A member of the series of order statistics (also called variational series) based on the results of observations. Let a random vector 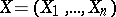 be observed which assumes values
be observed which assumes values 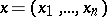 in an
in an  -dimensional Euclidean space
-dimensional Euclidean space 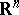 ,
, 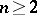 , and let, further, a function
, and let, further, a function 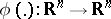 be given on
be given on 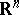 by the rule
by the rule
where 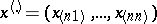 is a vector in
is a vector in  obtained from
obtained from  by rearranging its coordinates
by rearranging its coordinates  in ascending order of magnitude, i.e. the components
in ascending order of magnitude, i.e. the components 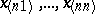 of the vector
of the vector  satisfy the relation
satisfy the relation
 | (1) |
In this case the statistic 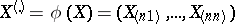 is the series (or vector) of order statistics, and its
is the series (or vector) of order statistics, and its 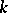 -th component
-th component 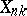 (
(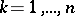 ) is called the
) is called the 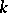 -th order statistic.
-th order statistic.
In the theory of order statistics the best studied case is the one where the components 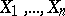 of the random vector
of the random vector 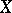 are independent random variables having the same distribution, as is assumed hereafter. If
are independent random variables having the same distribution, as is assumed hereafter. If 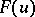 is the distribution function of the random variable
is the distribution function of the random variable 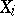 ,
, 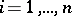 , then the distribution function
, then the distribution function 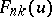 of the
of the 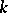 -th order statistic
-th order statistic 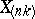 is given by the formula
is given by the formula
 | (2) |
where
is the incomplete beta-function. From (2) it follows that if the distribution function 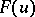 has probability density
has probability density 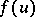 , then the probability density
, then the probability density 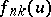 of the
of the 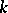 -th order statistic
-th order statistic 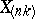 ,
, 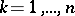 , also exists and is given by the formula
, also exists and is given by the formula
 | (3) |
Assuming the existence of the probability density 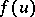 one obtains the joint probability density
one obtains the joint probability density 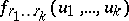 of the order statistics
of the order statistics 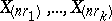 ,
, 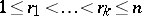 ,
, 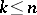 , which is given by the formula
, which is given by the formula
 | (4) |
The formulas (2)–(4) allow one, for instance, to find the distribution of the so-called extremal order statistics (or sample minimum and sample maximum)
and also the distribution of  , called the range statistic (or sample range). For instance, if the distribution function
, called the range statistic (or sample range). For instance, if the distribution function 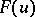 is continuous, then the distribution of
is continuous, then the distribution of 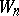 is given by
is given by
 | (5) |
Formulas (2)–(5) show that, as in the general theory of sampling methods, exact distributions of order statistics cannot be used to obtain statistical inferences if the distribution function 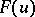 is unknown. It is precisely for this reason that asymptotic methods for the distribution functions of order statistics, as the dimension
is unknown. It is precisely for this reason that asymptotic methods for the distribution functions of order statistics, as the dimension  of the vector of observations tends to infinity, have been widely developed in the theory of order statistics. In the asymptotic theory of order statistics one studies the limit distributions of appropriately standardized sequences of order statistics
of the vector of observations tends to infinity, have been widely developed in the theory of order statistics. In the asymptotic theory of order statistics one studies the limit distributions of appropriately standardized sequences of order statistics 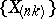 as
as 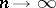 ; moreover, generally speaking, the order number
; moreover, generally speaking, the order number 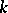 can change as a function of
can change as a function of  . If the order number
. If the order number 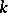 changes as
changes as  tends to infinity in such a way that the limit
tends to infinity in such a way that the limit 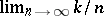 exists and is not equal to
exists and is not equal to  or to
or to 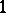 , then the corresponding order statistics
, then the corresponding order statistics  of the considered sequence
of the considered sequence 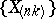 are called central or mean order statistics. If, however,
are called central or mean order statistics. If, however, 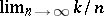 is equal to
is equal to  or to
or to 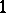 , then they are called extreme order statistics.
, then they are called extreme order statistics.
In mathematical statistics central order statistics are used to construct consistent sequences of estimators (cf. Consistent estimator) for quantiles (cf. Quantile) of the unknown distribution  based on the realization of a random vector
based on the realization of a random vector 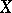 or, in other words, to estimate the function
or, in other words, to estimate the function 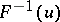 . For instance, let
. For instance, let 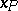 be a quantile of level
be a quantile of level 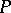 (
( ) of the distribution function
) of the distribution function 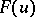 about which one knowns that its probability density
about which one knowns that its probability density 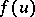 is continuous and strictly positive in some neighbourhood of the point
is continuous and strictly positive in some neighbourhood of the point 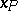 . In this case the sequence of central order statistics
. In this case the sequence of central order statistics 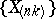 with order numbers
with order numbers 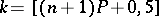 , where
, where 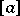 is the integer part of the real number
is the integer part of the real number  , is a sequence of consistent estimators for the quantiles
, is a sequence of consistent estimators for the quantiles 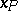 ,
, 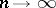 . Moreover, this sequence of order statistics
. Moreover, this sequence of order statistics 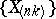 has an asymptotically normal distribution with parameters
has an asymptotically normal distribution with parameters
i.e. for any real 
 | (6) |
where 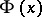 is the standard normal distribution function.
is the standard normal distribution function.
Example 1. Let 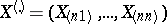 be a vector of order statistics based on a random vector
be a vector of order statistics based on a random vector 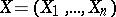 . The components of this vector are assumed to be independent random variables having the same probability distribution with a probability density that is continuous and positive in some neighbourhood of the median
. The components of this vector are assumed to be independent random variables having the same probability distribution with a probability density that is continuous and positive in some neighbourhood of the median 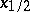 . In this case the sequence of sample medians
. In this case the sequence of sample medians 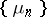 , defined for any
, defined for any 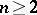 by
by
has an asymptotically normal distribution, as 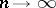 , with parameters
, with parameters
In particular, if
that is, 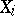 has the normal distribution
has the normal distribution 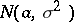 , then the sequence
, then the sequence 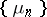 is asymptotically normally distributed with parameters
is asymptotically normally distributed with parameters 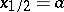 and
and 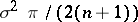 . If the sequence of statistics
. If the sequence of statistics 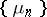 is compared with the sequence of best unbiased estimators (cf. Unbiased estimator)
is compared with the sequence of best unbiased estimators (cf. Unbiased estimator)
for the mean  of the normal distribution, then one should prefer the sequence
of the normal distribution, then one should prefer the sequence 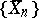 , since
, since
for any 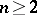 .
.
Example 2. Let 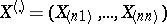 be the vector of order statistics based on the random vector
be the vector of order statistics based on the random vector 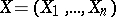 whose components are independent and uniformly distributed on an interval
whose components are independent and uniformly distributed on an interval 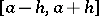 ; moreover, suppose that the parameters
; moreover, suppose that the parameters  and
and 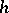 are unknown. In this case the sequences
are unknown. In this case the sequences 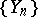 and
and 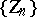 of statistics, where
of statistics, where
are consistent sequences of superefficient unbiased estimators (cf. Superefficient estimator) for  and
and 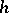 , respectively. Moreover,
, respectively. Moreover,
One can show that the sequences 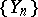 and
and 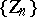 define the best estimators for
define the best estimators for  and
and 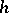 in the sense of the minimum of the square risk in the class of linear unbiased estimators expressed in terms of order statistics.
in the sense of the minimum of the square risk in the class of linear unbiased estimators expressed in terms of order statistics.
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | S.S. Wilks, "Mathematical statistics" , Princeton Univ. Press (1950) |
| [3] | H.A. David, "Order statistics" , Wiley (1970) |
| [4] | E.J. Gumble, "Statistics of extremes" , Columbia Univ. Press (1958) |
| [5] | J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967) |
| [6] | B.V. Gnedenko, "Limit theorems for the maximal term of a variational series" Dokl. Akad. Nauk SSSR , 32 : 1 (1941) pp. 7–9 (In Russian) |
| [7] | B.V. Gnedenko, "Sur la distribution limite du terme maximum d'une série aléatoire" Ann. of Math. , 44 : 3 (1943) pp. 423–453 |
| [8] | N.V. Smirnov, "Limit distributions for the terms of a variational series" Trudy Mat. Inst. Steklov. , 25 (1949) pp. 5–59 (In Russian) |
| [9] | N.V. Smirnov, "Some remarks on limit laws for order statistics" Theor. Probab. Appl. , 12 : 2 (1967) pp. 337–339 Teor. Veroyatnost. i Primenen. , 12 : 2 (1967) pp. 391–392 |
| [10] | D.M. Chibisov, "On limit distributions for order statistics" Theor. Probab. Appl. , 9 : 1 (1964) pp. 142–148 Teor. Veroyatnost. Primenen. , 9 : 1 (1964) pp. 159–165 |
| [11] | A.T. Craig, "On the distributions of certain statistics" Amer. J. Math. , 54 (1932) pp. 353–366 |
| [12] | L.H.C. Tippett, "On the extreme individuals and the range of samples taken from a normal population" Biometrika , 17 (1925) pp. 364–387 |
| [13] | E.S. Pearson, "The percentage limits for the distribution of ranges in samples from a normal population ( )" Biometrika , 24 (1932) pp. 404–417 )" Biometrika , 24 (1932) pp. 404–417 |
References
| [a1] | R.J. Serfling, "Approximation theorems of mathematical statistics" , Wiley (1980) |
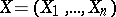 be observed which assumes values
be observed which assumes values 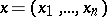 in an
in an  -dimensional Euclidean space
-dimensional Euclidean space 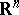 ,
, 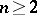 , and let, further, a function
, and let, further, a function 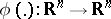 be given on
be given on 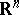 by the rule
by the rule
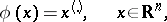
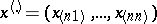 is a vector in
is a vector in  obtained from
obtained from  by rearranging its coordinates
by rearranging its coordinates  in ascending order of magnitude, i.e. the components
in ascending order of magnitude, i.e. the components 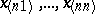 of the vector
of the vector  satisfy the relation
satisfy the relation

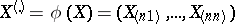 is the series (or vector) of order statistics, and its
is the series (or vector) of order statistics, and its 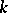 -th component
-th component 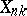 (
(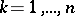 ) is called the
) is called the 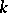 -th order statistic.
-th order statistic.
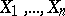 of the random vector
of the random vector 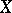 are independent random variables having the same distribution, as is assumed hereafter. If
are independent random variables having the same distribution, as is assumed hereafter. If 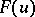 is the distribution function of the random variable
is the distribution function of the random variable 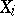 ,
, 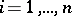 , then the distribution function
, then the distribution function 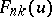 of the
of the 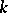 -th order statistic
-th order statistic 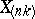 is given by the formula
is given by the formula

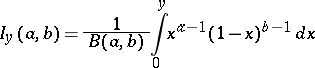
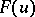 has probability density
has probability density 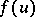 , then the probability density
, then the probability density 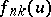 of the
of the 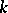 -th order statistic
-th order statistic 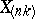 ,
, 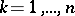 , also exists and is given by the formula
, also exists and is given by the formula

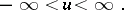
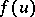 one obtains the joint probability density
one obtains the joint probability density 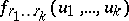 of the order statistics
of the order statistics 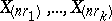 ,
, 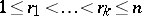 ,
, 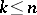 , which is given by the formula
, which is given by the formula

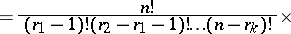
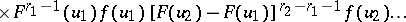
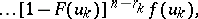
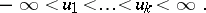
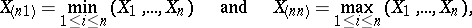
 , called the range statistic (or sample range). For instance, if the distribution function
, called the range statistic (or sample range). For instance, if the distribution function 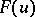 is continuous, then the distribution of
is continuous, then the distribution of 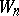 is given by
is given by

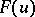 is unknown. It is precisely for this reason that asymptotic methods for the distribution functions of order statistics, as the dimension
is unknown. It is precisely for this reason that asymptotic methods for the distribution functions of order statistics, as the dimension  of the vector of observations tends to infinity, have been widely developed in the theory of order statistics. In the asymptotic theory of order statistics one studies the limit distributions of appropriately standardized sequences of order statistics
of the vector of observations tends to infinity, have been widely developed in the theory of order statistics. In the asymptotic theory of order statistics one studies the limit distributions of appropriately standardized sequences of order statistics 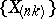 as
as 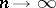 ; moreover, generally speaking, the order number
; moreover, generally speaking, the order number 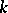 can change as a function of
can change as a function of  . If the order number
. If the order number 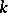 changes as
changes as  tends to infinity in such a way that the limit
tends to infinity in such a way that the limit 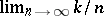 exists and is not equal to
exists and is not equal to  or to
or to 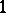 , then the corresponding order statistics
, then the corresponding order statistics  of the considered sequence
of the considered sequence 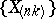 are called central or mean order statistics. If, however,
are called central or mean order statistics. If, however, 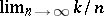 is equal to
is equal to  or to
or to 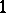 , then they are called extreme order statistics.
, then they are called extreme order statistics.
 based on the realization of a random vector
based on the realization of a random vector 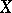 or, in other words, to estimate the function
or, in other words, to estimate the function 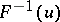 . For instance, let
. For instance, let 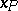 be a quantile of level
be a quantile of level 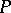 (
( ) of the distribution function
) of the distribution function 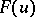 about which one knowns that its probability density
about which one knowns that its probability density 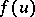 is continuous and strictly positive in some neighbourhood of the point
is continuous and strictly positive in some neighbourhood of the point 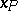 . In this case the sequence of central order statistics
. In this case the sequence of central order statistics 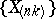 with order numbers
with order numbers 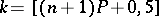 , where
, where 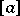 is the integer part of the real number
is the integer part of the real number  , is a sequence of consistent estimators for the quantiles
, is a sequence of consistent estimators for the quantiles 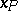 ,
, 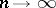 . Moreover, this sequence of order statistics
. Moreover, this sequence of order statistics 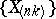 has an asymptotically normal distribution with parameters
has an asymptotically normal distribution with parameters
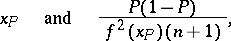


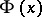 is the standard normal distribution function.
is the standard normal distribution function.
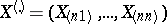 be a vector of order statistics based on a random vector
be a vector of order statistics based on a random vector 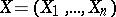 . The components of this vector are assumed to be independent random variables having the same probability distribution with a probability density that is continuous and positive in some neighbourhood of the median
. The components of this vector are assumed to be independent random variables having the same probability distribution with a probability density that is continuous and positive in some neighbourhood of the median 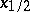 . In this case the sequence of sample medians
. In this case the sequence of sample medians 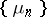 , defined for any
, defined for any 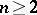 by
by
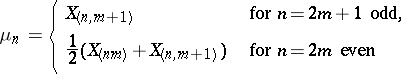
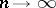 , with parameters
, with parameters
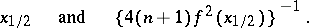
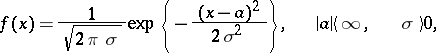
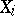 has the normal distribution
has the normal distribution 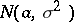 , then the sequence
, then the sequence 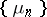 is asymptotically normally distributed with parameters
is asymptotically normally distributed with parameters 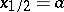 and
and 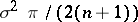 . If the sequence of statistics
. If the sequence of statistics 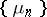 is compared with the sequence of best unbiased estimators (cf. Unbiased estimator)
is compared with the sequence of best unbiased estimators (cf. Unbiased estimator)
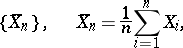
 of the normal distribution, then one should prefer the sequence
of the normal distribution, then one should prefer the sequence 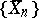 , since
, since
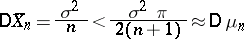
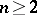 .
.
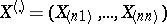 be the vector of order statistics based on the random vector
be the vector of order statistics based on the random vector 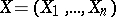 whose components are independent and uniformly distributed on an interval
whose components are independent and uniformly distributed on an interval 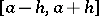 ; moreover, suppose that the parameters
; moreover, suppose that the parameters  and
and 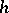 are unknown. In this case the sequences
are unknown. In this case the sequences 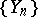 and
and 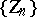 of statistics, where
of statistics, where
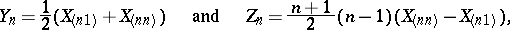
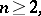
 and
and  , respectively. Moreover,
, respectively. Moreover,
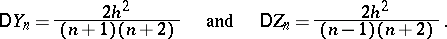
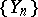 and
and 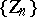 define the best estimators for
define the best estimators for  and
and 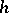 in the sense of the minimum of the square risk in the class of linear unbiased estimators expressed in terms of order statistics.
in the sense of the minimum of the square risk in the class of linear unbiased estimators expressed in terms of order statistics.
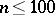 )" Biometrika , 24 (1932) pp. 404–417
)" Biometrika , 24 (1932) pp. 404–417