One-parameter subgroup
of a Lie group  over a normed field
over a normed field 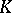
An analytic homomorphism of the additive group of the field 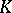 into
into 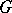 , that is, an analytic mapping
, that is, an analytic mapping 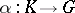 such that
such that
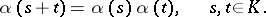 |
The image of this homomorphism, which is a subgroup of 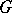 , is also called a one-parameter subgroup. If
, is also called a one-parameter subgroup. If 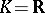 , then the continuity of the homomorphism
, then the continuity of the homomorphism 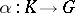 implies that it is analytic. If
implies that it is analytic. If 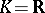 or
or 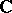 , then for any tangent vector
, then for any tangent vector 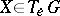 to
to 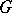 at the point
at the point  there exists a unique one-parameter subgroup
there exists a unique one-parameter subgroup 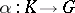 having
having 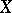 as its tangent vector at the point
as its tangent vector at the point 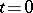 . Here
. Here 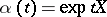 ,
, 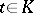 , where
, where 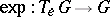 is the exponential mapping. In particular, any one-parameter subgroup of the general linear group
is the exponential mapping. In particular, any one-parameter subgroup of the general linear group 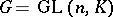 has the form
has the form
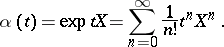 |
If 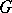 is a real Lie group endowed with a two-sidedly invariant pseudo-Riemannian metric or affine connection, then the one-parameter subgroups of
is a real Lie group endowed with a two-sidedly invariant pseudo-Riemannian metric or affine connection, then the one-parameter subgroups of 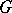 are the geodesics passing through the identity
are the geodesics passing through the identity  .
.
References
| [1] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [2] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [3] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
Comments
References
| [a1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [a2] | N. Bourbaki, "Groupes et algèbres de Lie" , Hermann (1972) pp. Chapt. 2; 3 |
| [a3] | G. Hochschild, "Structure of Lie groups" , Holden-Day (1965) |
One-parameter subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=One-parameter_subgroup&oldid=11235