Octahedron
A solid figure having eight triangular faces, twelve edges and six vertices, with 4 faces at each vertex. If all edges have the same length, it is one of the five regular polyhedra (Platonic solids); if the edge length is  , then the volume of the octahedron is
, then the volume of the octahedron is
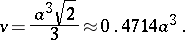 |

Figure: o068100a
Comments
The Schläfli symbol of an octahedron is 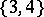 . When the edges all have the same length one deals with the regular octahedron, reciprocal to the cube; it can be regarded either as a triangular anti-prism or as a square double-pyramid. As one of the five Platonic polyhedra (cf. Regular polyhedra; Platonic solids) it represents the ancient element air. It occurs in nature as a crystal of chrome alum. In terms of its circumradius as unit of measurement, its six vertices have Cartesian coordinates
. When the edges all have the same length one deals with the regular octahedron, reciprocal to the cube; it can be regarded either as a triangular anti-prism or as a square double-pyramid. As one of the five Platonic polyhedra (cf. Regular polyhedra; Platonic solids) it represents the ancient element air. It occurs in nature as a crystal of chrome alum. In terms of its circumradius as unit of measurement, its six vertices have Cartesian coordinates
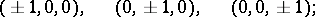 |
thus it has edge-length 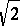 , inradius
, inradius 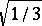 and volume
and volume 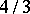 . Its 4 pairs of opposite faces (or the 4 diameters of the cube) are freely permuted by the octahedral group
. Its 4 pairs of opposite faces (or the 4 diameters of the cube) are freely permuted by the octahedral group 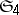 of order
of order  .
.
References
| [a1] | G.T. Bennett, "Deformable octahedra" Proc. London Math. Soc. (2) , 10 (1912) pp. 309–343 |
| [a2] | H.S.M. Coxeter, "Regular polytopes" , Methuen (1948) pp. 5 |
Octahedron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Octahedron&oldid=14196