Normal scheme

A scheme all local rings (cf. Local ring) of which are normal (that is, reduced and integrally closed in their ring of fractions). A normal scheme is locally irreducible; for such a scheme the concepts of a connected component and an irreducible component are the same. The set of singular points of a Noetherian normal scheme has codimension greater than 1. The following normality criterion holds [1]: A Noetherian scheme is normal if and only if two conditions are satisfied: 1) for any point of codimension the local ring is regular (cf. Regular ring (in commutative algebra)); and 2) for any point of codimension the depth of the ring (cf. Depth of a module) is greater than 1. Every reduced scheme has a normal scheme canonically connected with it (normalization). The 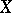-scheme 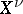is integral, but not always finite over . However, if 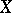is excellent (see Excellent ring), for example, if 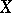is a scheme of finite type over a field, then 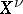is finite over .

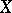References

[1]	J.-P. Serre, "Algèbre locale. Multiplicités" , Lect. notes in math. , 11 , Springer (1975)

Comments

A normalization of an irreducible algebraic variety 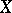is an irreducible normal variety 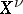together with a regular mapping 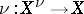that is finite and a birational isomorphism.

For an affine irreducible algebraic variety, 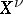is the integral closure of the ring 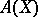of regular functions on 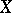in its field of fractions. The normalization has the following universality properties. Let 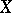be an integral scheme (i.e. 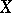is both reduced and irreducible, or, equivalently, 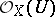is an integral domain for all ope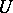n in 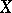). For every normal integral scheme 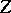and every dominant morphism 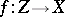(i.e. 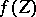is dense in 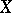), 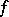factors uniquely through the normalization 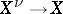. So also Normal analytic space.

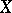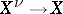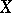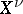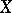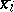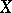Let be a curve and a, possibly singular, point on . Let be the normalization of and the inverse images of in . These points are called the branches of passing through . The terminology derives from the fact that the can be identified (in the case of varieties over or ) with the "branches" of passing through . More precisely, if the 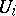are sufficiently small complex or real neighbourhoods of the 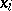, then some neighbourhood of is the union of the branches 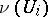. Let 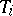be the tangent space at to . Then 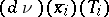is some linear subspace of the tangent space to at . It will be either a line or a point. In the first case the branch 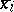is called linear. The point 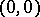on 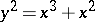is an example of a point with two linear branches (with tangents , 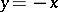), and the point 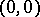on 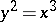gives an example of a two-fold non-linear branch.

References

[a1]	R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91
[a2]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1974) pp. Sect. II.5 (Translated from Russian)
[a3]	H. Matsumura, "Commutative algebra" , Benjamin (1970)