Normal operator

A closed linear operator defined on a linear subspace that is dense in a Hilbert space such that , where is the operator adjoint to . If is normal, then and for every . Conversely, these conditions guarantee that 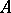is normal. If 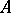is normal, then so are ; for any 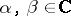; 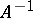when it exists; and if , where 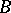is a bounded linear operator, then also .

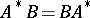A normal operator has:

1) the multiplicative decomposition

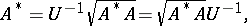where 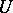is a unitary operator which is uniquely determined on the orthogonal complement of the null space of 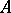and ;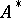

2) the additive decomposition

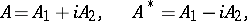where 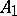and 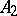are uniquely determined self-adjoint commuting operators.

The additive decomposition implies that for an ordered pair 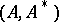there exists a unique two-dimensional spectral function 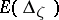, where 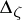is a two-dimensional interval, 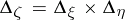, , 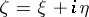such that

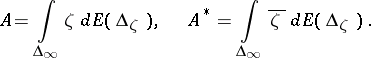The same decomposition also implies that a normal operator 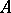is a function of a certain self-adjoint operator 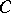, 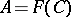. Conversely, every function of some self-adjoint operator is normal.

An important property of a normal operator 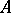is the fact that 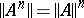, which implies that the spectral radius of a normal operator 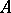is its norm 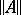. Eigen elements of a normal operator corresponding to distinct eigen values are orthogonal.

References

[1]	A.I. Plesner, "Spectral theory of linear operators" , F. Ungar (1965) (Translated from Russian)
[2]	W. Rudin, "Functional analysis" , McGraw-Hill (1973)

References

[a1]	J.B. Conway, "Subnormal operators" , Pitman (1981)