Non-linear operator
A mapping 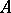 of a space (as a rule, a vector space)
of a space (as a rule, a vector space) 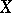 into a vector space
into a vector space 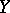 over a common field of scalars that does not have the property of linearity, that is, such that generally speaking
over a common field of scalars that does not have the property of linearity, that is, such that generally speaking
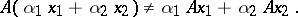 |
If 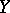 is the set
is the set  of real or
of real or 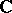 of complex numbers, then a non-linear operator is called a non-linear functional. The simplest example of a non-linear operator (non-linear functional) is a real-valued function of a real argument other than a linear function. One of the important sources of the origin of non-linear operators are problems in mathematical physics. If in a local mathematical description of a process small quantities not only of the first but also of higher orders are taken into account, then there arise equations with non-linear operators. Certain problems in mathematical economics, auto-regulation, control theory, etc., also lead to non-linear operator equations.
of complex numbers, then a non-linear operator is called a non-linear functional. The simplest example of a non-linear operator (non-linear functional) is a real-valued function of a real argument other than a linear function. One of the important sources of the origin of non-linear operators are problems in mathematical physics. If in a local mathematical description of a process small quantities not only of the first but also of higher orders are taken into account, then there arise equations with non-linear operators. Certain problems in mathematical economics, auto-regulation, control theory, etc., also lead to non-linear operator equations.
Examples of non-linear operators.
1)
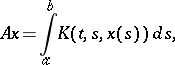 |
where 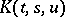 ,
, 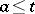 ,
, 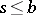 ,
, 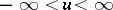 , is a function such that
, is a function such that 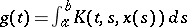 is continuous on
is continuous on 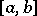 for any
for any 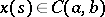 (for example,
(for example, 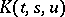 is continuous on
is continuous on 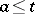 ,
, 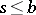 ,
, 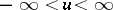 ). If
). If 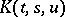 is non-linear in
is non-linear in  , then
, then  is a non-linear Urysohn operator mapping
is a non-linear Urysohn operator mapping 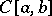 into itself. Under other restrictions on
into itself. Under other restrictions on 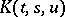 an Urysohn operator acts on other spaces, for instance,
an Urysohn operator acts on other spaces, for instance, 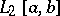 or maps one Orlicz space
or maps one Orlicz space 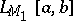 into another
into another 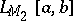 .
.
2)
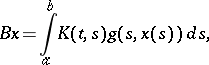 |
where 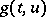 is non-linear in
is non-linear in  and defined for
and defined for 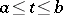 ,
, 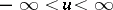 . Under appropriate restrictions on
. Under appropriate restrictions on 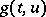 the operator
the operator 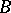 acts from one function space into another and is called a non-linear Hammerstein operator.
acts from one function space into another and is called a non-linear Hammerstein operator.
3)
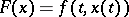 |
is a superposition operator, also called a Nemytskii operator, and, under suitable restrictions on the non-linearity in the second argument of the function, it transforms the space of measurable functions 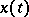 into itself.
into itself.
4)
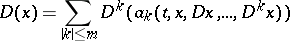 |
is a non-linear differential operator of order 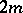 in divergence form acting on the Sobolev space
in divergence form acting on the Sobolev space 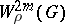 under suitable restrictions on the non-linear function
under suitable restrictions on the non-linear function 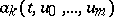 . Here
. Here 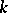 is the multi-index
is the multi-index 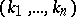 ,
, 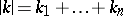 ,
, 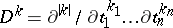 and
and  is a bounded domain in
is a bounded domain in 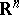 .
.
5)
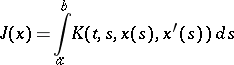 |
is non-linear integro-differential operator acting under appropriate restrictions on the function 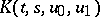 in the space
in the space 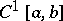 of continuously-differentiable functions.
of continuously-differentiable functions.
To non-linear operators acting from one topological vector space 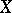 into another one
into another one 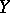 , many concepts and operations of mathematical analysis of real-valued functions of a real variable can be transferred. Thus, a non-linear operator
, many concepts and operations of mathematical analysis of real-valued functions of a real variable can be transferred. Thus, a non-linear operator 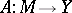 ,
, 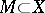 , is called bounded if
, is called bounded if 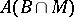 is a bounded set in
is a bounded set in 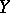 for any bounded set
for any bounded set 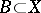 ; a non-linear operator
; a non-linear operator 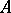 is continuous at a point
is continuous at a point 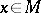 if the inverse image
if the inverse image 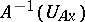 of a neighbourhood
of a neighbourhood 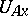 of the point
of the point 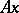 contains
contains 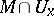 for some neighbourhood
for some neighbourhood  of
of  . As for functions, a non-linear operator that is continuous at every point of a compact set
. As for functions, a non-linear operator that is continuous at every point of a compact set 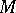 is bounded on this set. In contrast to linear operators, if a non-linear operator
is bounded on this set. In contrast to linear operators, if a non-linear operator 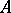 acting on a normed space is bounded on some ball, it does not follow that
acting on a normed space is bounded on some ball, it does not follow that 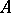 is continuous on this ball. However, in certain cases continuity (boundedness) of a non-linear operator on a ball implies continuity (boundedness) of the operator in its whole domain of definition.
is continuous on this ball. However, in certain cases continuity (boundedness) of a non-linear operator on a ball implies continuity (boundedness) of the operator in its whole domain of definition.
Among the non-linear operators acting from 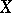 to
to 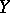 one can distinguish certain important classes.
one can distinguish certain important classes.
1) Semi-linear operators  , linear in each argument. The space
, linear in each argument. The space 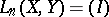 of all
of all  -linear operators is isomorphic to the space
-linear operators is isomorphic to the space 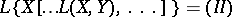 , where
, where 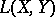 is the space of all linear operators from
is the space of all linear operators from 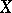 to
to 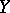 . If
. If 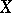 and
and 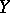 are normed spaces, then
are normed spaces, then  and
and 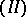 are isometric. If
are isometric. If 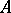 is symmetric in all arguments, then
is symmetric in all arguments, then 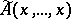 is denoted by
is denoted by 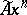 and is called a homogeneous operator of degree
and is called a homogeneous operator of degree  .
.
2) In spaces endowed with a partial order, isotone operators 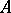 and antitone operators
and antitone operators 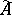 are characterized by the conditions
are characterized by the conditions  and
and 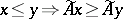 .
.
3) In a Hilbert space 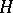 , monotone operators
, monotone operators 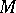 are defined by the condition
are defined by the condition 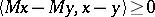 for any
for any 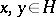 .
.
4) Compact operators transform bounded subsets in the domain of definition into pre-compact sets; among them are the completely-continuous operators, which are simultaneously compact and continuous.
For non-linear operators the concepts of a differential and a derivative are non-trivial and useful. An operator 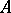 acting from an open set
acting from an open set 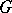 of a normed vector space
of a normed vector space 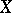 into a normed vector space
into a normed vector space 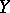 is called Fréchet differentiable at a point
is called Fréchet differentiable at a point  if there exists a continuous linear operator
if there exists a continuous linear operator  such that for any
such that for any 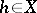 for which
for which 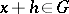 ,
,
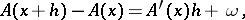 |
where 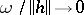 as
as 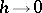 . In this case the linear part
. In this case the linear part 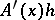 in
in 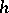 of the increment
of the increment 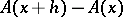 is called the Fréchet differential of
is called the Fréchet differential of 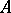 at
at  and is denoted by
and is denoted by 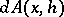 , and
, and  is called the remainder of the increment. The bounded linear operator
is called the remainder of the increment. The bounded linear operator 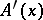 is called the Fréchet derivative of
is called the Fréchet derivative of  at
at  . Apart from Fréchet differentiability one also introduces Gâteaux differentiability. Namely, an operator
. Apart from Fréchet differentiability one also introduces Gâteaux differentiability. Namely, an operator 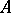 is called Gâteaux differentiable at a point
is called Gâteaux differentiable at a point  if the limit
if the limit
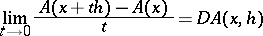 |
exists, which is called the Gâteaux differential of 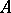 at
at  . The Gâteaux differential is homogeneous in
. The Gâteaux differential is homogeneous in 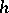 , that is,
, that is, 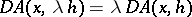 . If
. If 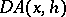 is linear in
is linear in 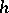 and
and  , then the linear operator
, then the linear operator 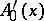 is called the Gâteaux derivative of
is called the Gâteaux derivative of 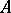 . Fréchet differentiability implies Gâteaux differentiability, and then
. Fréchet differentiability implies Gâteaux differentiability, and then  . Gâteaux differentiability does not, in general, imply Fréchet differentiability, but if
. Gâteaux differentiability does not, in general, imply Fréchet differentiability, but if 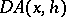 exists in a neighbourhood of
exists in a neighbourhood of  , is continuous in
, is continuous in 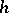 and uniformly continuous in
and uniformly continuous in  , then
, then 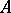 is Fréchet differentiable at
is Fréchet differentiable at  . For non-linear functionals
. For non-linear functionals  Fréchet and Gâteaux differentials and derivatives are defined similarly. Here the Gâteaux derivative
Fréchet and Gâteaux differentials and derivatives are defined similarly. Here the Gâteaux derivative 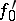 is called the gradient of the functional
is called the gradient of the functional  and is an operator from
and is an operator from 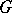 to
to 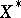 . If
. If 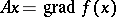 for some non-linear functional
for some non-linear functional 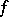 , then
, then 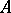 is called a potential operator.
is called a potential operator.
For operators acting on separable topological vector spaces one can in one way or another define differentiation. Let 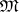 be a collection of bounded sets in a topological vector space
be a collection of bounded sets in a topological vector space 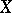 . A mapping
. A mapping 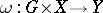 is called
is called  -small if
-small if 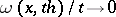 as
as 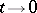 uniformly in
uniformly in  for any
for any 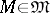 . A mapping
. A mapping 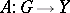 (where
(where 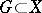 is open) is called
is open) is called 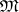 -differentiable at
-differentiable at  if
if
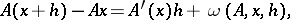 |
where 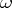 is an
is an 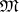 -small mapping. Most frequently
-small mapping. Most frequently 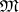 is taken to be the collection of all bounded, all compact or all finite sets of
is taken to be the collection of all bounded, all compact or all finite sets of  . For non-linear operators on normed spaces the first case leads to Fréchet differentiability and the third to Gâteaux differentiability.
. For non-linear operators on normed spaces the first case leads to Fréchet differentiability and the third to Gâteaux differentiability.
Higher-order derivatives 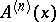 and
and 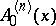 of an operator
of an operator 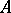 are defined in the usual way, as derivatives of derivatives. These are symmetric multi-linear mappings. A differential of order
are defined in the usual way, as derivatives of derivatives. These are symmetric multi-linear mappings. A differential of order  is then a homogeneous form
is then a homogeneous form  of degree
of degree  . Other definitions of higher-order derivatives are possible. Suppose, for example, that
. Other definitions of higher-order derivatives are possible. Suppose, for example, that 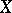 and
and 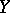 are normed vector spaces,
are normed vector spaces, 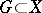 is open, and
is open, and 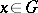 . If for any
. If for any 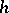 for which
for which 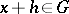 ,
,
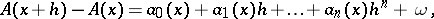 | (*) |
where 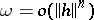 , then the multi-linear form
, then the multi-linear form 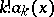 is called the derivative of order
is called the derivative of order 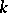 . The expression (*) is then called the bounded expansion of order
. The expression (*) is then called the bounded expansion of order  of the difference
of the difference 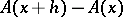 . Under appropriate restrictions the various definitions of higher-order derivatives are equivalent.
. Under appropriate restrictions the various definitions of higher-order derivatives are equivalent.
If a scalar countably-additive measure is given in 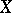 , then a non-linear operator can be integrated, by understanding
, then a non-linear operator can be integrated, by understanding 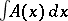 in the sense of the Bochner integral.
in the sense of the Bochner integral.
For a non-linear operator 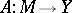 , as in the case of a linear operator, the values of the parameter
, as in the case of a linear operator, the values of the parameter 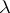 for which
for which  exists and is continuous on
exists and is continuous on 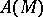 are naturally called regular, and the remaining points
are naturally called regular, and the remaining points 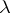 belong to the spectrum. In its properties the spectrum of a non-linear operator
belong to the spectrum. In its properties the spectrum of a non-linear operator 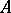 can differ vastly from spectra of linear operators. Thus, the spectrum of a completely-continuous non-linear operator can have continuous parts; an eigen element
can differ vastly from spectra of linear operators. Thus, the spectrum of a completely-continuous non-linear operator can have continuous parts; an eigen element 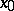 of an operator
of an operator 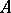 , that is, an element
, that is, an element 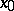 such that
such that 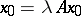 , can bifurcate into several eigen element branches (as
, can bifurcate into several eigen element branches (as 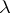 varies), cf. Bifurcation.
varies), cf. Bifurcation.
References
| [1] | L.A. Lyusternik, V.I. Sobolev, "Elemente der Funktionalanalysis" , Akademie Verlag (1968) (Translated from Russian) |
| [2] | L.V. Kantorovich, G.P. Akilov, "Functionalanalysis in normierten Räumen" , Akademie Verlag (1964) (Translated from Russian) |
| [3] | M.M. Vainberg, "Variational methods for the study of nonlinear operators" , Holden-Day (1964) (Translated from Russian) |
| [4] | M.A. Krasnosel'skii, P.P. Zabreiko, "Geometric methods of non-linear analysis" , Springer (1983) (Translated from Russian) |
| [5] | H. Gajewski, K. Gröger, K. Zacharias, "Nichtlineare Operatorgleichungen und Operatordifferentialgleichungen" , Akademie Verlag (1974) |
Non-linear operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-linear_operator&oldid=14292