Non-holonomic systems
Systems of material points that are subject to constraints among which are kinematic constraints that impose conditions on the velocities (and not only the positions) of the points of the system in its possible positions (see Holonomic system); these conditions are assumed to be expressible as non-integrable differential relations
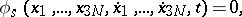 | (1) |
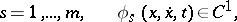 |
that cannot be replaced by equivalent finite relationships among the coordinates. Here, the 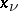 denote the Cartesian coordinates of the points,
denote the Cartesian coordinates of the points, 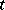 is the time and
is the time and 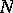 is the number of points in the system. Most often one considers constraints (1) that are linear in the velocities
is the number of points in the system. Most often one considers constraints (1) that are linear in the velocities  , of the form
, of the form
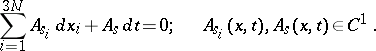 |
The constraints (1) are said to be stationary if 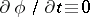 . These constraints also impose conditions on the accelerations
. These constraints also impose conditions on the accelerations 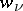 of the points:
of the points:
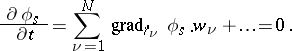 |
Following N.G. Chetaev [2], assume that the possible motions of the systems subject to the non-linear constraints (1) satisfy conditions of the type
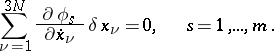 | (2) |
In the case of linear constraints, these conditions imply the usual relations
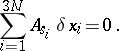 |
Unlike the situation in holonomic systems, motion between neighbouring positions at an infinitesimally-small distance from one another may be impossible in a non-holonomic system (see [1]).
In generalized Lagrange coordinates, equations (1) and (2) are written as
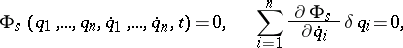 |
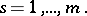 |
In a non-holonomic system, the number 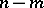 of degrees of freedom is less than the number
of degrees of freedom is less than the number  of independent coordinates
of independent coordinates 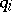 by the number
by the number 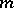 of non-integrable constraint equations.
of non-integrable constraint equations.
Many and varied forms of differential equations of motion have been derived for non-holonomic systems, such as the Lagrange equation of the first kind (cf. Lagrange equations (in mechanics)), the Appell equations in Lagrange coordinates and quasi-coordinates, the Chaplygin–Voronets equations in Lagrange coordinates, the Boltzmann equation, the Hamel equation in quasi-coordinates, etc. (see [3]).
A characteristic feature of non-holonomic systems is that, in the general case, their differential equations of motion include the constraint equations.
References
| [1] | H. Hertz, "The principles of mechanics presented in a new form" , Dover (1956) (Translated from German) |
| [2] | N.G. Chetaev, Izv. Fiz.-Mat. Obshch. Kazan. Univ. (3) , 6 (1932) pp. 68–71 |
| [3] | Yu.I. Neimark, N.A. Fufaev, "Dynamics of nonholonomic systems" , Amer. Math. Soc. (1972) (Translated from Russian) |
Comments
References
| [a1] | L.D. Landau, E.M. Lifshitz, "Course of theoretical physics" , 1. Mechanics , Pergamon (1976) |
| [a2] | E.G.G. Sudarshan, "Classical dynamics: a modern perspective" , Wiley (Interscience) (1974) |
Non-holonomic systems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-holonomic_systems&oldid=12986