Newton binomial
binomium of Newton
The formula for the expansion of an arbitrary positive integral power of a binomial in a polynomial arranged in powers of one of the terms of the binomial:
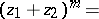 | (*) |
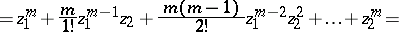 |
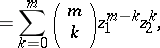 |
where
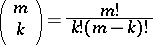 |
are the binomial coefficients. For  terms formula (*) takes the form
terms formula (*) takes the form
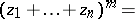 |
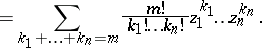 |
For an arbitrary exponent  , real or even complex, the right-hand side of (*) is, generally speaking, a binomial series.
, real or even complex, the right-hand side of (*) is, generally speaking, a binomial series.
The gradual mastering of binomial formulas, beginning with the simplest special cases (formulas for the "square" and the "cube of a sum" ) can be traced back to the 11th century. I. Newton's contribution, strictly speaking, lies in the discovery of the binomial series.
Comments
The coefficients
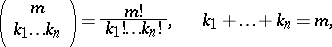 |
are called multinomial coefficients.
Newton binomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Newton_binomial&oldid=13002