Neumann function
From Encyclopedia of Mathematics
A cylinder function (cf. Cylinder functions) of the second kind. The Neumann functions  (occasionally the notation
(occasionally the notation  is used) can be defined in terms of the Bessel functions as follows:
is used) can be defined in terms of the Bessel functions as follows:
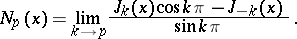 |
They are real for positive real  and tend to zero as
and tend to zero as  . For large
. For large  they have the asymptotic representation
they have the asymptotic representation
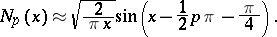 |
They are connected by the recurrence formulas
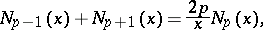 |
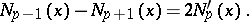 |
For integers  :
:
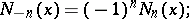 |
for small  :
:
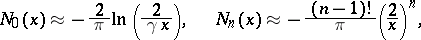 |
where 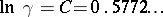 is the Euler constant.
is the Euler constant.
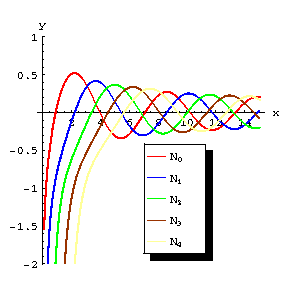
Figure: n066420a
Graphs of Neumann functions.
The Neumann functions of "half-integral" order 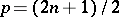 can be expressed in terms of the trigonometric functions; in particular,
can be expressed in terms of the trigonometric functions; in particular,
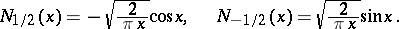 |
They were introduced by C.G. Neumann in 1867.
For references see Cylinder functions.
How to Cite This Entry:
Neumann function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Neumann_function&oldid=17802
Neumann function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Neumann_function&oldid=17802
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article