Mumford hypothesis
The hypothesis that each semi-simple algebraic group 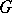 is geometrically reductive, i.e., has the following property: For any rational representation of
is geometrically reductive, i.e., has the following property: For any rational representation of 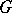 in a finite-dimensional vector space
in a finite-dimensional vector space 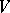 and any non-zero vector
and any non-zero vector 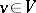 fixed by
fixed by 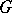 , there is a
, there is a 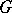 -invariant homogeneous polynomial
-invariant homogeneous polynomial 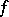 of positive degree on
of positive degree on 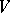 for which
for which 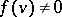 .
.
This hypothesis was stated by D. Mumford [1] (in a different, but equivalent form) with the aim of finding a property of semi-simple groups, defined over an algebraically closed field of arbitrary characteristic, which, from the point of view of the geometric theory of invariants (cf. Invariants, theory of), would serve as a substitute for the classical property of complete reducibility of rational linear representations of semi-simple groups defined over fields of characteristic zero (this latter property not holding for ground fields of positive characteristic). It would allow the removal of restrictions on the characteristic of the ground field in a number of central results in the geometric theory of invariants, such as the theorem on finite generation of the algebra of invariants of reductive groups of automorphisms of an algebra of finite type over a field (see Hilbert theorem on invariants).
If the characteristic of the ground field 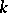 is zero, then a proof of Mumford's hypothesis is given by Weyl's classical theorem on complete reducibility of rational representations of semi-simple groups (see [2]): in this case the invariant line
is zero, then a proof of Mumford's hypothesis is given by Weyl's classical theorem on complete reducibility of rational representations of semi-simple groups (see [2]): in this case the invariant line 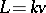 in
in 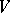 has an invariant complement
has an invariant complement 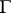 (an invariant hyperplane such that
(an invariant hyperplane such that 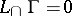 ), and
), and 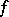 can be taken to be the linear form giving the equation of
can be taken to be the linear form giving the equation of 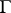 . When
. When 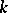 has positive characteristic
has positive characteristic 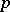 , Mumford's hypothesis generalizes the fact that there is an invariant homogeneous hypersurface
, Mumford's hypothesis generalizes the fact that there is an invariant homogeneous hypersurface 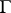 in
in 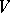 for which
for which 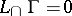 (with the degree of
(with the degree of 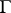 equal to
equal to 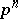 for some integer
for some integer  ).
).
Mumford's hypothesis is also equivalent to the assertion that for any regular action of a semi-simple group 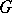 on an affine algebraic variety
on an affine algebraic variety 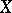 and for any two closed non-intersecting invariant subsets
and for any two closed non-intersecting invariant subsets 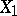 and
and 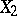 in
in 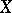 there is an invariant regular function
there is an invariant regular function 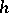 on
on 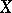 for which
for which 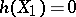 and
and 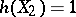 (i.e.,
(i.e., 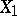 and
and 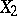 can be separated by regular invariants, see [3]).
can be separated by regular invariants, see [3]).
Mumford's hypothesis was first proved in [4]; the proof was extended in [5] to the general case of reductive group schemes over a field.
The proof of Mumford's hypothesis, together with the results of [6] and [10], allow one, first, to give a final form to the generalization of Hilbert's theorem on invariants: If 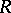 is an algebra of finite type over an algebraically closed field
is an algebra of finite type over an algebraically closed field 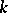 ,
, 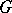 is a reductive group, acting as an automorphism group on
is a reductive group, acting as an automorphism group on 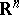 , and
, and 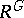 is the subalgebra of all
is the subalgebra of all  -invariant elements in
-invariant elements in 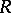 , then
, then 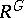 is also an algebra of finite type over
is also an algebra of finite type over 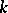 ; and, secondly, to establish that a linear algebraic group over a field of arbitrary characteristic is geometrically reductive if and only if it is reductive (cf. Reductive group). Mumford's hypothesis has applications in the geometric theory of invariants and in moduli theory (see [7]–[9]).
; and, secondly, to establish that a linear algebraic group over a field of arbitrary characteristic is geometrically reductive if and only if it is reductive (cf. Reductive group). Mumford's hypothesis has applications in the geometric theory of invariants and in moduli theory (see [7]–[9]).
References
| [1] | D. Mumford, "Geometric invariant theory" , Springer (1965) |
| [2] | J. Fogarty, "Invariant theory" , Benjamin (1969) |
| [3] | J. Dieudonné, J.B. Carrell, "Invariant theory: old and new" , Acad. Press (1971) |
| [4] | W.J. Haboush, "Reductive groups are geometrically reductive" Ann. of Math. , 102 (1975) pp. 67–83 |
| [5] | C.S. Seshadri, "Geometric reductivity over arbitrary base" Adv. Math. , 26 (1977) pp. 225–274 |
| [6] | M. Nagata, "Invariants of a group in an affine ring" J. Math. Kyoto Univ. , 3 (1964) pp. 369–377 (With appendix by M. Miyanishi) |
| [7] | C.S. Seshadri, "Mumford's conjecture for 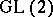 and applications" , Algebraic geometry. Papers presented at the Bombay Colloq. 1968 , Oxford Univ. Press (1969) pp. 347–371 and applications" , Algebraic geometry. Papers presented at the Bombay Colloq. 1968 , Oxford Univ. Press (1969) pp. 347–371 |
| [8] | H. Popp, "Moduli theory and classification theory of algebraic varieties" , Springer (1977) |
| [9] | C.S. Seshadri, "Theory of moduli" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1975) pp. 263–304 |
| [10] | M. Nagata, T. Miyata, "Note on semi-reductive groups" J. Math. Kyoto Univ. , 3 (1964) pp. 379–382 |
Mumford hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mumford_hypothesis&oldid=11673