Multilinear mapping
 -linear mapping, multilinear operator
-linear mapping, multilinear operator
A mapping 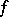 of the direct product
of the direct product 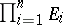 of unitary modules
of unitary modules 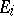 (cf. Unitary module) over a commutative associative ring
(cf. Unitary module) over a commutative associative ring 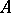 with a unit into a certain
with a unit into a certain 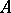 -module
-module 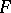 which is linear in each argument, i.e. which satisfies the condition
which is linear in each argument, i.e. which satisfies the condition
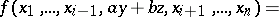 |
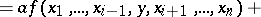 |
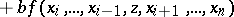 |
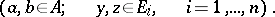 |
In the case 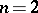 (
( ) one speaks of a bilinear mapping (respectively, a trilinear mapping). Each multilinear mapping
) one speaks of a bilinear mapping (respectively, a trilinear mapping). Each multilinear mapping
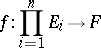 |
defines a unique linear mapping 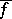 of the tensor product
of the tensor product 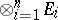 into
into 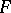 such that
such that
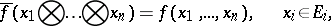 |
where the correspondence  is a bijection of the set of multilinear mappings
is a bijection of the set of multilinear mappings 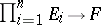 into the set of all linear mappings
into the set of all linear mappings 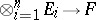 . The multilinear mappings
. The multilinear mappings 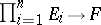 naturally form an
naturally form an  -module.
-module.
On the 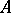 -module
-module 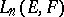 of all
of all  -linear mappings
-linear mappings 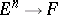 there acts the symmetric group
there acts the symmetric group 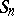 :
:
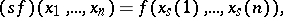 |
where 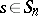 ,
, 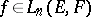 ,
, 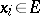 . A multilinear mapping
. A multilinear mapping  is called symmetric if
is called symmetric if 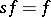 for all
for all 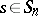 , and skew-symmetric if
, and skew-symmetric if 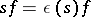 , where
, where 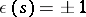 in accordance with the sign of the permutation
in accordance with the sign of the permutation  . A multilinear mapping is called sign-varying (or alternating) if
. A multilinear mapping is called sign-varying (or alternating) if 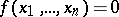 when
when  for some
for some 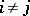 . Any alternating multilinear mapping is skew-symmetric, while if in
. Any alternating multilinear mapping is skew-symmetric, while if in 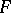 the equation
the equation 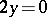 has the unique solution
has the unique solution 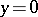 the converse also holds. The symmetric multilinear mappings form a submodule in
the converse also holds. The symmetric multilinear mappings form a submodule in 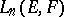 that is naturally isomorphic to the module of linear mappings
that is naturally isomorphic to the module of linear mappings 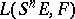 , where
, where 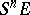 is the
is the  -th symmetric power of
-th symmetric power of  (see Symmetric algebra). The alternating multilinear mappings form a submodule that is naturally isomorphic to
(see Symmetric algebra). The alternating multilinear mappings form a submodule that is naturally isomorphic to 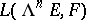 , where
, where 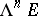 is the
is the  -th exterior power of the module
-th exterior power of the module 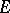 (see Exterior algebra). The multilinear mapping
(see Exterior algebra). The multilinear mapping 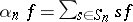 is called the symmetrized multilinear mapping defined by
is called the symmetrized multilinear mapping defined by 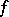 , while the multilinear mapping
, while the multilinear mapping 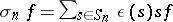 is called the skew-symmetrized mapping defined by
is called the skew-symmetrized mapping defined by 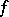 . Symmetrized (skew-symmetrized) multilinear mappings are symmetric (respectively, alternating), and if in
. Symmetrized (skew-symmetrized) multilinear mappings are symmetric (respectively, alternating), and if in 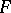 the equation
the equation 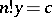 has a unique solution for each
has a unique solution for each 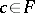 , then the converse is true. A sufficient condition for any alternating multilinear mapping to be a skew-symmetrization is that the module
, then the converse is true. A sufficient condition for any alternating multilinear mapping to be a skew-symmetrization is that the module  is free (cf. Free module). For references see Multilinear form.
is free (cf. Free module). For references see Multilinear form.
Multilinear mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multilinear_mapping&oldid=15130