Morse inequalities
Inequalities following from Morse theory and relating the number of critical points (cf. Critical point) of a Morse function on a manifold to its homology invariants.
Let 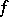 be a Morse function on a smooth
be a Morse function on a smooth  -dimensional manifold
-dimensional manifold  (without boundary) having a finite number of critical points. Then the homology group
(without boundary) having a finite number of critical points. Then the homology group 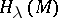 is finitely generated and is therefore determined by its rank,
is finitely generated and is therefore determined by its rank,  , and its torsion rank,
, and its torsion rank, 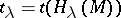 (the torsion rank of an Abelian group
(the torsion rank of an Abelian group 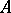 with a finite number of generators is the minimal number of cyclic groups in a direct-sum decomposition of which a maximal torsion subgroup of
with a finite number of generators is the minimal number of cyclic groups in a direct-sum decomposition of which a maximal torsion subgroup of  can be imbedded). The Morse inequalities relate the number
can be imbedded). The Morse inequalities relate the number 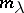 of critical points of
of critical points of  with Morse index
with Morse index  to these ranks, and have the form:
to these ranks, and have the form:
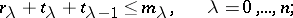 |
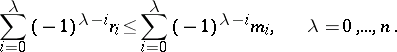 |
For  the last Morse inequality is always an equality, so that
the last Morse inequality is always an equality, so that
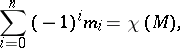 |
where 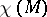 is the Euler characteristic of
is the Euler characteristic of 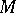 .
.
The Morse inequalities also hold for Morse functions of a triple 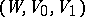 , it suffices to replace the groups
, it suffices to replace the groups 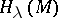 by the relative homology groups
by the relative homology groups 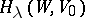 .
.
According to the Morse inequalities, a manifold having "large" homology groups does not admit a Morse function with a small number of critical points. It is remarkable that the estimates in the Morse inequalities are sharp: On a closed simply-connected manifold of dimension 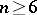 there is a Morse function for which the Morse inequalities are equalities (Smale's theorem, see [2]). In particular, on any closed manifold that is homotopically equivalent to the sphere
there is a Morse function for which the Morse inequalities are equalities (Smale's theorem, see [2]). In particular, on any closed manifold that is homotopically equivalent to the sphere 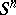 , with
, with 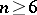 , there is a Morse function with two critical points; hence it follows immediately (see Morse theory) that
, there is a Morse function with two critical points; hence it follows immediately (see Morse theory) that 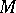 is homeomorphic to
is homeomorphic to 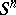 (see Poincaré conjecture). A similar application of Smale's theorem allows one to prove theorems on
(see Poincaré conjecture). A similar application of Smale's theorem allows one to prove theorems on  - and
- and  -cobordism.
-cobordism.
An analogue of the Morse inequalities holds for a Morse function 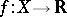 on an infinite-dimensional Hilbert manifold, and they relate (for any regular values
on an infinite-dimensional Hilbert manifold, and they relate (for any regular values 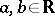 ,
, 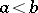 , of
, of  ) the numbers
) the numbers 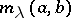 of critical points of finite index
of critical points of finite index  lying in
lying in 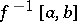 , with the rank
, with the rank 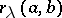 and torsion rank
and torsion rank 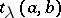 of the group
of the group  , where
, where 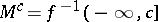 . Namely,
. Namely,
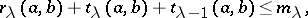 |
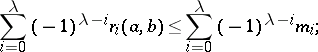 |
 |
For 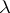 large enough the latter inequality becomes an equality.
large enough the latter inequality becomes an equality.
References
| [1] | M. Morse, "The calculus of variations in the large" , Amer. Math. Soc. (1934) |
| [2] | S. Smale, "Generalized Poincaré's conjecture in dimensions greater than four" Ann. of Math. , 74 (1961) pp. 391–466 |
Comments
Another version of the Morse inequalities can be stated as follows, cf. [a1].
For a Morse function 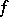 one introduces the quantity
one introduces the quantity
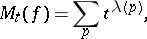 |
where the sum is taken over the critical points 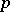 of
of 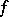 and
and 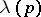 is the index of
is the index of 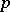 relative to
relative to  . In the compact case this sum is finite, since the critical points are discrete. The polynomial
. In the compact case this sum is finite, since the critical points are discrete. The polynomial 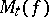 , which is also called the Morse polynomial of
, which is also called the Morse polynomial of  , has the Poincaré polynomial of the manifold
, has the Poincaré polynomial of the manifold 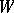 as a lower bound in the following sense. Let
as a lower bound in the following sense. Let
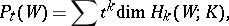 |
where the homology is taken relative to some fixed coefficient field 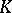 . Then the following Morse inequality holds: For every non-degenerate
. Then the following Morse inequality holds: For every non-degenerate 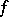 there exists a polynomial
there exists a polynomial  with non-negative coefficients such that
with non-negative coefficients such that
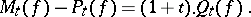 |
References
| [a1] | R. Bott, "Lectures on Morse theory, old and new" Bull. Amer. Math. Soc. , 7 : 2 (1982) pp. 331–358 |
| [a2] | J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) |
| [a3] | R.S. Palais, "Morse theory on Hilbert manifolds" Topology , 2 (1963) pp. 299–340 |
Morse inequalities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morse_inequalities&oldid=17143