Moment matrix
A matrix containing the moments of a probability distribution (cf. also Moment; Moments, method of (in probability theory)). For example, if  is a probability distribution on a set
is a probability distribution on a set  , then
, then  is its
is its  th order moment. If
th order moment. If  and thus the moments are given, then a linear functional
and thus the moments are given, then a linear functional  is defined on the set of polynomials by
is defined on the set of polynomials by  ,
,  . The inverse problem is called a moment problem (cf. also Moment problem): Given the sequence of moments
. The inverse problem is called a moment problem (cf. also Moment problem): Given the sequence of moments  ,
, 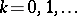 , find the necessary and sufficient conditions for the existence of and an expression for a positive distribution (a non-decreasing function with possibly infinitely many points of increase) that gives the integral representation of that linear functional. A positive distribution can only exist if
, find the necessary and sufficient conditions for the existence of and an expression for a positive distribution (a non-decreasing function with possibly infinitely many points of increase) that gives the integral representation of that linear functional. A positive distribution can only exist if 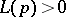 for any polynomial
for any polynomial 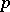 that is positive on
that is positive on 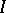 .
.
For the Hamburger moment problem (cf. also Complex moment problem, truncated), 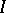 is the real axis and the polynomials are real, so the functional
is the real axis and the polynomials are real, so the functional 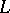 is positive if
is positive if 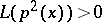 for any non-zero polynomial
for any non-zero polynomial 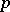 and this implies that the moment matrices, i.e., the Hankel matrices of the moment sequence,
and this implies that the moment matrices, i.e., the Hankel matrices of the moment sequence, 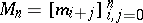 , are positive definite for all
, are positive definite for all 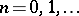 (cf. also Hankel matrix). This is a necessary and sufficient condition for the existence of a solution.
(cf. also Hankel matrix). This is a necessary and sufficient condition for the existence of a solution.
For the trigonometric moment problem, 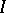 is the unit circle in the complex plane and the polynomials are complex, so that "positive definite" here means that
is the unit circle in the complex plane and the polynomials are complex, so that "positive definite" here means that 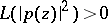 for all non-zero polynomials
for all non-zero polynomials 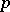 . The linear functional is automatically defined on the space of Laurent polynomials (cf. also Laurent series) since
. The linear functional is automatically defined on the space of Laurent polynomials (cf. also Laurent series) since  . Positive definite now corresponds to the Toeplitz moment matrices
. Positive definite now corresponds to the Toeplitz moment matrices 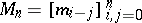 being positive definite for all
being positive definite for all 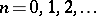 (cf. also Toeplitz matrix). Again this is the necessary and sufficient condition for the existence of a (unique) solution to the moment problem.
(cf. also Toeplitz matrix). Again this is the necessary and sufficient condition for the existence of a (unique) solution to the moment problem.
Once the positive-definite linear functional is given, one can define an inner product on the space of polynomials as 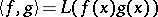 in the real case or as
in the real case or as 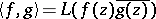 in the complex case. The moment matrix is then the Gram matrix for the standard basis
in the complex case. The moment matrix is then the Gram matrix for the standard basis 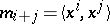 or
or 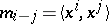 .
.
Generalized moments correspond to the use of non-standard basis functions for the polynomials or for possibly other spaces. Consider a set of basis functions 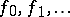 that span the space
that span the space 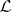 . The modified or generalized moments are then given by
. The modified or generalized moments are then given by  . The moment problem is to find a positive distribution function
. The moment problem is to find a positive distribution function 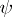 that gives an integral representation of the linear functional on
that gives an integral representation of the linear functional on 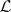 . However, to define an inner product, one needs the functional to be defined on
. However, to define an inner product, one needs the functional to be defined on 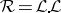 (in the real case) or on
(in the real case) or on 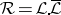 (in the complex case). This requires a doubly indexed sequence of "moments"
(in the complex case). This requires a doubly indexed sequence of "moments"  . Finding a distribution for an integral representation of
. Finding a distribution for an integral representation of 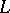 on
on 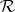 is called a strong moment problem.
is called a strong moment problem.
The solution of moment problems is often obtained using an orthogonal basis. If the 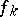 are orthonormalized to give the functions
are orthonormalized to give the functions 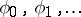 , then the moment matrix
, then the moment matrix 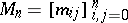 can be used to give explicit expressions; namely
can be used to give explicit expressions; namely 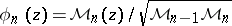 where
where 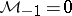 ,
, 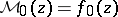 and for
and for 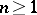 ,
, 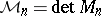 with
with
 |
The leading coefficient in the expansion 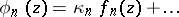 satisfies
satisfies 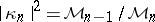 .
.
References
| [a1] | N.I. Akhiezer, "The classical moment problem" , Oliver & Boyd (1969) (In Russian) |
| [a2] | J.A. Shohat, J.D. Tamarkin, "The problem of moments" , Math. Surveys , 1 , Amer. Math. Soc. (1943) (In Russian) |
Moment matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Moment_matrix&oldid=15678