Model theory
The part of mathematical logic studying mathematical models (cf. Model (in logic)).
The origins of model theory go back to the 1920's and 1930's, when the following two fundamental theorems were proved.
Theorem 1
(Gödel compactness theorem). If each finite subcollection of a collection $T$ of propositions in a first-order language is consistent, then the whole collection $T$ is consistent (see [1]).
Theorem 2
(Löwenheim–Skolem theorem). If a collection of propositions in a first-order language of signature  has an infinite model, then it has a model of any infinite cardinality not less than the cardinality of
has an infinite model, then it has a model of any infinite cardinality not less than the cardinality of  .
.
Theorem 1 has had extensive application in algebra. On the basis of this theorem, A.I. Mal'tsev created a method of proof of local theorems in algebra (see Mal'tsev local theorems).
Let  be an algebraic system of signature
be an algebraic system of signature  , let
, let 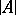 be the underlying set of
be the underlying set of  , let
, let 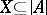 , let
, let 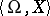 denote the signature obtained from
denote the signature obtained from  by the addition of symbols for distinguished elements
by the addition of symbols for distinguished elements 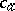 for all
for all 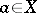 , and let
, and let 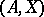 denote the algebraic system of signature
denote the algebraic system of signature 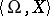 which is an enrichment of
which is an enrichment of 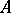 in which for each
in which for each 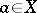 the symbol
the symbol 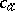 is interpreted by the element
is interpreted by the element  . The set
. The set 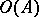 of all closed formulas of the signature
of all closed formulas of the signature 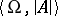 in a first-order language which are true in the system
in a first-order language which are true in the system 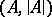 is called the elementary diagram of the algebraic system
is called the elementary diagram of the algebraic system 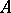 (or the description of the algebraic system
(or the description of the algebraic system 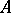 ), and the set
), and the set 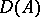 of those formulas from
of those formulas from 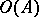 which are either atomic or the negation of an atomic formula is called the diagram of
which are either atomic or the negation of an atomic formula is called the diagram of 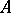 . An algebraic system
. An algebraic system 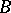 is called an elementary extension of
is called an elementary extension of 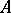 if
if 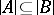 and if
and if 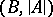 is a model for
is a model for 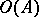 . In this case
. In this case 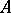 is called an elementary subsystem of
is called an elementary subsystem of 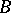 . For example, the set of rational numbers with the usual order relation is an elementary subsystem of the system of real numbers with the usual order relation.
. For example, the set of rational numbers with the usual order relation is an elementary subsystem of the system of real numbers with the usual order relation.
A subsystem 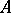 of an algebraic system
of an algebraic system  of signature
of signature  is an elementary subsystem of
is an elementary subsystem of 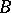 if and only if for each closed formula
if and only if for each closed formula 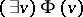 in the first-order language of signature
in the first-order language of signature 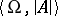 which is true in
which is true in 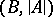 there is an
there is an 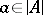 such that
such that 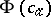 is true in
is true in 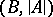 . It follows at once from this criterion that the union of an increasing chain of elementary subsystems is an elementary extension of each of these subsystems. If a closed
. It follows at once from this criterion that the union of an increasing chain of elementary subsystems is an elementary extension of each of these subsystems. If a closed 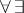 -formula in a first-order language is true in every system of an increasing chain of systems, then it is true in the union of the chain (see [1], [8]).
-formula in a first-order language is true in every system of an increasing chain of systems, then it is true in the union of the chain (see [1], [8]).
Let the signature  contain a one-place relation symbol
contain a one-place relation symbol 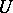 . One says that a model
. One says that a model 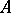 of a theory
of a theory 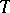 of signature
of signature  has type
has type 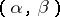 if the cardinality of
if the cardinality of 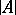 is equal to
is equal to 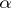 and if the cardinality of
and if the cardinality of 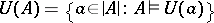 is equal to
is equal to 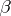 . Vaught's theorem: If an elementary theory
. Vaught's theorem: If an elementary theory 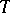 of countable signature has a model of type
of countable signature has a model of type 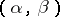 where
where  , then
, then 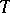 has a model of type
has a model of type 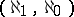 (see [7], [8], [10]). Under the assumption that the generalized continuum hypothesis holds, an elementary theory of countable signature has models of types
(see [7], [8], [10]). Under the assumption that the generalized continuum hypothesis holds, an elementary theory of countable signature has models of types 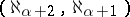 for each
for each 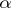 , if it has a model of type
, if it has a model of type 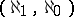 (see [10]). Under the same assumption the theory
(see [10]). Under the same assumption the theory 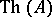 , where the signature of
, where the signature of 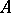 is
is 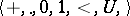 ,
, 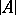 is the set of all real numbers,
is the set of all real numbers, 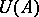 the set of all integers, and
the set of all integers, and 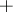 ,
,  ,
,  ,
, 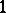 ,
, 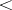 are defined in the usual way, does not have a model of type
are defined in the usual way, does not have a model of type 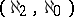 .
.
Let 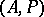 denote the enrichment of the algebraic system
denote the enrichment of the algebraic system 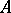 by a predicate
by a predicate 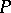 , and let
, and let 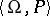 be the signature obtained from
be the signature obtained from  by the addition of the predicate symbol
by the addition of the predicate symbol 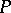 . In many cases it is important to understand when in each member of a class
. In many cases it is important to understand when in each member of a class 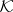 of algebraic systems of signature
of algebraic systems of signature 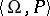 the predicate
the predicate 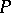 is given by a formula in the first-order language of the signature
is given by a formula in the first-order language of the signature  . A partial answer to this question is given by Beth's definability theorem: There exists a formula
. A partial answer to this question is given by Beth's definability theorem: There exists a formula  in the first-order language of signature
in the first-order language of signature  such that the formula
such that the formula 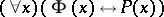 is true for all members of an axiomatizable class
is true for all members of an axiomatizable class 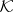 of signature
of signature 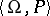 if and only if the set
if and only if the set 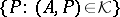 contains at most one element for each algebraic system
contains at most one element for each algebraic system 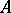 of signature
of signature  (see [2], [8]).
(see [2], [8]).
Much research in model theory is connected with the study of properties preserved under operations on algebraic systems. The most important operations include homomorphism, direct and filtered products.
A statement 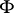 is said to be stable with respect to homomorphisms if the truth of
is said to be stable with respect to homomorphisms if the truth of 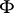 in an algebraic system
in an algebraic system 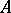 implies the truth of
implies the truth of 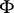 in all epimorphic images of
in all epimorphic images of 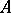 . A formula
. A formula 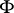 in a first-order language is called positive if
in a first-order language is called positive if 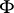 does not contain negation and implication signs. It has been proved (see [1], [8]) that a statement
does not contain negation and implication signs. It has been proved (see [1], [8]) that a statement 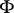 in a first-order language is stable relative to homomorphisms if and only if
in a first-order language is stable relative to homomorphisms if and only if 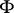 is equivalent to a positive statement. A similar theorem holds for the language
is equivalent to a positive statement. A similar theorem holds for the language 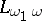 .
.
A formula 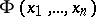 in a first-order language of signature
in a first-order language of signature  is called a Horn formula it it can be obtained by conjunction and quantification from formulas of the form
is called a Horn formula it it can be obtained by conjunction and quantification from formulas of the form 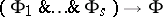 ,
, 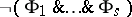 , where
, where 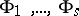 are atomic formulas in the first-order language of
are atomic formulas in the first-order language of  . Examples of Horn formulas are identities and quasi-identities. Central in the theory of ultraproducts is the theorem of J. Łos: Every formula in a first-order language is stable with respect to any ultrafilter (see [1]). A formula in a first-order language is conditionally stable with respect to any filter if and only if it is equivalent to a Horn formula. There is the following theorem (see [9]): Two algebraic systems
. Examples of Horn formulas are identities and quasi-identities. Central in the theory of ultraproducts is the theorem of J. Łos: Every formula in a first-order language is stable with respect to any ultrafilter (see [1]). A formula in a first-order language is conditionally stable with respect to any filter if and only if it is equivalent to a Horn formula. There is the following theorem (see [9]): Two algebraic systems 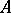 and
and 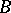 of signature
of signature  are elementarily equivalent if and only if there is an ultrafilter
are elementarily equivalent if and only if there is an ultrafilter 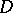 on a set
on a set 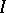 such that
such that 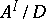 and
and 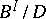 are isomorphic. The cardinality of a filtered product is countably infinite if for each natural number
are isomorphic. The cardinality of a filtered product is countably infinite if for each natural number  the number of factors of cardinality
the number of factors of cardinality  is finite. If for each natural number
is finite. If for each natural number  the set of indices for which the corresponding factors have cardinality
the set of indices for which the corresponding factors have cardinality  does not belong to
does not belong to 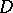 , then the cardinality of the ultraproduct with respect to a non-principal ultrafilter
, then the cardinality of the ultraproduct with respect to a non-principal ultrafilter 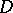 on a countable set
on a countable set 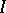 is equal to that of the continuum. For each infinite set
is equal to that of the continuum. For each infinite set 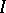 of cardinality
of cardinality 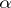 there is a filter
there is a filter 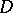 on
on  such that for each filter
such that for each filter 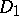 on
on 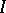 containing
containing 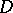 , and each infinite set
, and each infinite set 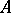 , the cardinality of
, the cardinality of 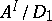 is not less than
is not less than 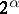 (see [1]).
(see [1]).
Many applications have been found for the Ehrenfeucht–Mostowski theorem on the existence of models with a large number of automorphisms (see [3]): For any totally ordered set 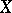 in an axiomatizable class
in an axiomatizable class 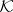 of algebraic systems containing an infinite system, there is a system
of algebraic systems containing an infinite system, there is a system 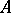 such that
such that 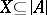 and such that each order-preserving one-to-one mapping of
and such that each order-preserving one-to-one mapping of 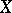 onto
onto 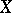 can be extended to an automorphism of
can be extended to an automorphism of 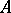 .
.
The major notions in model theory are those of universal, homogeneous and saturated systems. Let 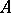 and
and 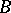 be algebraic systems of a signature
be algebraic systems of a signature  . A mapping
. A mapping 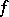 of a set
of a set 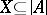 into a set
into a set  is called elementary if for each formula
is called elementary if for each formula 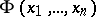 in the first-order language of the signature
in the first-order language of the signature  and any
and any 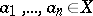 the equivalence
the equivalence 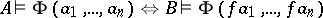 holds. A system
holds. A system 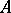 is called
is called 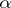 -universal if for every system
-universal if for every system 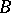 that is elementarily equivalent to
that is elementarily equivalent to 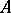 and of cardinality not exceeding
and of cardinality not exceeding 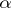 , there is an elementary mapping from
, there is an elementary mapping from 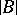 into
into 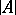 . A system
. A system 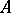 is called
is called 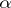 -homogeneous if for every set
-homogeneous if for every set 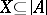 of cardinality less than
of cardinality less than 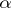 , every elementary mapping from
, every elementary mapping from 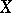 into
into 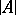 can be extended to an elementary mapping of
can be extended to an elementary mapping of 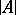 onto
onto 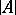 (that is, to an automorphism of
(that is, to an automorphism of 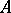 ). A system
). A system 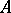 of signature
of signature  is called
is called 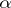 -saturated if for every set
-saturated if for every set 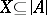 of cardinality less than
of cardinality less than 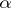 and every collection
and every collection 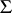 of formulas in the first-order language of the signature
of formulas in the first-order language of the signature 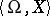 not containing free variables other than
not containing free variables other than 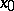 ,
, 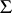 finitely satisfiable in
finitely satisfiable in 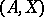 implies that
implies that 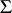 is satisfiable in
is satisfiable in 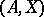 . A system is called universal (respectively, homogeneous or saturated) if
. A system is called universal (respectively, homogeneous or saturated) if 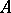 is
is 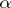 -universal (respectively,
-universal (respectively, 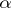 -homogeneous or
-homogeneous or 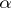 -saturated), where
-saturated), where 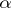 is the cardinality of
is the cardinality of 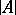 . A system is saturated if and only if it is simultaneously universal and homogeneous. Two elementary equivalent saturated systems of the same cardinality are isomorphic (see [3]). All uncountable models of elementary theories which are categorical in uncountable cardinalities (cf. Categoricity in cardinality) and of countable signature are saturated (Morley's theorem, see [3], [8]). A large number of examples of
. A system is saturated if and only if it is simultaneously universal and homogeneous. Two elementary equivalent saturated systems of the same cardinality are isomorphic (see [3]). All uncountable models of elementary theories which are categorical in uncountable cardinalities (cf. Categoricity in cardinality) and of countable signature are saturated (Morley's theorem, see [3], [8]). A large number of examples of 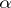 -saturated systems is given by ultraproducts. For example, if
-saturated systems is given by ultraproducts. For example, if 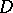 is a non-principal ultrafilter on a countable set
is a non-principal ultrafilter on a countable set 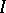 , then
, then 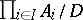 is an
is an 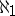 -saturated system for any algebraic system
-saturated system for any algebraic system 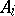 (
(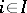 ) of a countable signature
) of a countable signature  .
.
The basic problems of model theory are the study of the expressive possibilities of a formalized language and the study of classes of structures defined by means of such a language. Some important properties of stable theories have been found, and the classes of categorical and superstable theories have been studied in even more detail.
The basic apparatus for the study of stable theories is the classification of formulas and locally consistent sets of formulas in these theories. Such a classification can be obtained by means of ascribing to formulas their ranks. Such ranks are usually ordinals and the ranking functions are given with the help of special topologies and other means. The study of ranking functions and their improvements is a rich source of information on the theories.
In the study of classes of models one is concerned with the number of distinct models, up to isomorphism, of a theory of a given cardinality, the existence of special models, for example, simple, minimal, saturated, homogeneous, universal, etc., and one creates means for constructing them.
The classical examples of application of methods of model theory are the papers of A. Robinson and his school, which developed an independent science — non-standard analysis; from the work of Mal'tsev and his school the applications of model-theoretic methods to topological algebra have been developed; the latest results on the properties of stable theories have been used in the study of concrete algebraic questions.
The above problems arose also in the study of various non-elementary languages, for example, obtained by the addition of new quantifiers, the introduction of infinite expressions, modalities, etc.
References
| [1] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
| [2] | A. Robinson, "Introduction to model theory and to the metamathematics of algebra" , North-Holland (1963) |
| [3] | M.A. Taitslin, "Model theory" , Novosibirsk (1970) (In Russian) |
| [4] | Yu.L. Ershov, "Decidability problems and constructive models" , Moscow (1980) (In Russian) |
| [5] | Yu.A. Palyutin, "Mathematical logic" , Moscow (1979) (In Russian) |
| [6] | Yu.L. Ershov, I.A. Lavrov, A.D. Taimanov, M.A. Taitslin, "Elementary theories" Russian Math. Surveys , 20 : 4 (1965) pp. 35–105 Uspekhi Mat. Nauk , 20 : 4 (1965) pp. 37–108 |
| [7] | A.I. Mal'tsev, "Some problems in the theory of classes of models" , Proc. 4-th All-Union Math. Congress (1961) , 1 , Leningrad (1963) pp. 169–198 (In Russian) (Transl. in: Amer. Math. Soc. Transl. (2) 83 (1969), 1–48) |
| [8] | C.C. Chang, H.J. Keisler, "Model theory" , North-Holland (1973) |
| [9] | G.E. Sacks, "Saturated model theory" , Benjamin (1972) |
| [10] | R.L. Vaught, "Denumerable models of complete theories" , Infinitistic methods. Proc. Symp. Foundations of Math. Warsaw, 1959 , Pergamon (1961) pp. 303–321 |
| [11] | M. Morley, R. Vaught, "Homogeneous universal models" Math. Scand. , 11 : 1 (1962) pp. 37–57 |
| [12] | M. Morley, "Categoricity in power" Trans. Amer. Math. Soc. , 114 : 2 (1965) pp. 514–538 |
| [13] | S. Shelah, "Classification theory and the number of non-isomorphic models" , North-Holland (1978) |
| [14] | J.L. Bell, A.B. Slomson, "Models and ultraproducts: an introduction" , North-Holland (1971) |
Comments
Theorem 1 was proved by K. Gödel in [a1].
Let 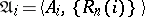 ,
, 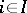 , be a collection of relational structures of the same type (algebraic systems of the same signature). (I.e. the
, be a collection of relational structures of the same type (algebraic systems of the same signature). (I.e. the 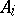 are sets, the
are sets, the 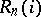 relations.) Let
relations.) Let 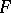 be an ultrafilter on the index set
be an ultrafilter on the index set 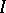 . Then the ultraproduct
. Then the ultraproduct 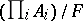 is a relational structure of the same type. (Cf. (the editorial comments to) Ultrafilter for the definition of ultraproduct.)
is a relational structure of the same type. (Cf. (the editorial comments to) Ultrafilter for the definition of ultraproduct.)
A precise formulation of Łos' theorem is now as follows (cf. [a8] or [a9]). Let 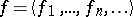 be a sequence of elements from
be a sequence of elements from 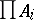 , i.e.
, i.e. 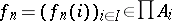 for all
for all  . Let
. Let 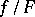 be the sequence
be the sequence 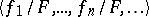 of elements from
of elements from 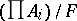 and let
and let 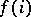 be the sequence
be the sequence 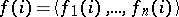 . Then for any formula
. Then for any formula  from the language
from the language 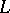 for which the
for which the 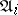 are interpretations,
are interpretations,
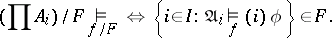 |
Łos' theorem is also called the fundamental theorem on ultraproducts.
The theorem to the effect that two algebraic systems 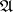 and
and 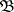 are equivalent if and only if they have isomorphic ultrapowers is known as the Keisler ultrapower theorem.
are equivalent if and only if they have isomorphic ultrapowers is known as the Keisler ultrapower theorem.
One of the basic applications of logic to algebra is the work by J. Ax and S. Kochen [a2].
See [a3] for the model theory of infinitary languages; [a4], [a5] for stability theory; and [a6], [a7] for categorical model theory.
The Gödel compactness theorem and the Löwenheim–Skolem theorem are in the Russian literature sometimes known as the Gödel–Mal'tsev theorem and the Löwenheim–Skolem–Mal'tsev theorem, respectively.
References
| [a1] | K. Gödel, "Die Vollständigheit der Axiome des logischen Funktionenkalküls" Monatshefte für Math. und Physik , 37 (1930) pp. 344–360 |
| [a2] | J. Ax, S. Kochen, "Diophantine problems over local fields III: decidable fields" Ann. of Math. , 83 (1966) pp. 437–456 |
| [a3] | M.A. Dickmann, "Large infinitary languages" , North-Holland (1975) |
| [a4] | A. Pillay, "An introduction to stability theory" , Oxford Univ. Press (1985) |
| [a5] | J.T. Baldwin, "Fundamentals of stability theory" , Springer (1988) |
| [a6] | G.E. Reges, "First order categorical logic" , Lect. notes in math. , 611 , Springer (1977) |
| [a7] | J. Lambek, P. Scott, "Higher order categorical logic" , Cambridge Univ. Press (1986) |
| [a8] | J.L. Bell, A.B. Slomson, "Models and ultraproducts" , North-Holland (1969) |
| [a9] | W.W. Comfort, S. Negrepontis, "The theory of ultrafilters" , Springer (1974) pp. §11 |
Model theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Model_theory&oldid=30755