Minkowski problem

Does there exist a closed convex hyperplane for which the Gaussian curvature is a given function of the unit outward normal ? This problem was posed by H. Minkowski [1], to whom is due a generalized solution of the problem in the sense that it contains no information on the nature of regularity of 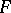, even if 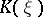is an analytic function. He proved that if a continuous positive function , given on the hypersphere , satisfies the condition

(1)

then there exists a closed convex surface 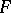, which is moreover unique (up to a parallel translation), for which 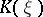is the Gaussian curvature at a point with outward normal .

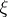A regular solution of Minkowski's problem has been given by A.V. Pogorelov in 1971 (see [2]); he also considered certain questions in geometry and in the theory of differential equations bordering on this problem. Namely, he proved that if 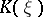is of class 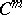, , 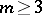then the surface 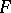is of class 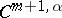, , 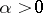and if 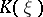is analytic, then 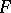also turns out to be analytic.

A natural generalization of Minkowski's problem is the solution of the question of the existence of convex hypersurfaces with given elementary symmetric principal curvature functions 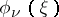of any given order , 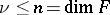. In particular, for 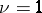this is Christoffel's problem on the recovery of a surface from its mean curvature. A necessary condition for the solvability of this generalized Minkowski problem, analogous to (1), has the form

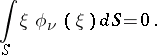However, this condition is not sufficient (A.D. Aleksandrov, 1938, see [3]). There are examples of sufficient conditions:

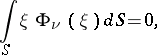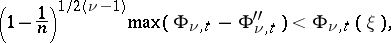where 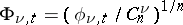, , 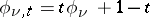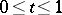. Here the regularity of is as in the Minkowski problem. Using approximations these results turn out to be valid even for functions 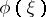which are non-negative, symmetric and concave.

References

[1]	H. Minkowski, "Volumen und Oberfläche" Math. Ann. , 57 (1903) pp. 447–495
[2]	A.V. Pogorelov, "The Minkowski multidimensional problem" , Winston (1978) (Translated from Russian)
[3]	H. Busemann, "Convex surfaces" , Interscience (1958)

References

[a1]	A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1973) (Translated from Russian)
[a2]	M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)
[a3]	R. Schneider, "Boundary structure and curvature of convex bodies" J. Tölke (ed.) J.M. Wills (ed.) , Contributions to geometry , Birkhäuser (1979) pp. 13–59