Minimal polynomial of a matrix
From Encyclopedia of Mathematics
minimum polynomial of a matrix
Let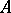 
be a matrix. The minimal polynomial of 
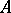is the monic polynomial 
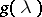of lowest degree such that 
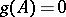. It divides the characteristic polynomial of 
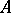and, more generally, it divides every polynomial 
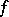such that 
.
References
| [a1] | L. Mirsky, "An introduction to linear algebra" , Dover, reprint (1990) pp. 203ff |
| [a2] | Ch.G. Cullen, "Matrices and linear transformations" , Dover, reprint (1990) pp. 178ff |
How to Cite This Entry:
Minimal polynomial of a matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_polynomial_of_a_matrix&oldid=16850
Minimal polynomial of a matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_polynomial_of_a_matrix&oldid=16850
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article