Metric
distance on a set 
A function  with non-negative real values, defined on the Cartesian product
with non-negative real values, defined on the Cartesian product  and satisfying for any
and satisfying for any  the conditions:
the conditions:
1)  if and only if
if and only if  (the identity axiom);
(the identity axiom);
2)  (the triangle axiom);
(the triangle axiom);
3)  (the symmetry axiom).
(the symmetry axiom).
A set  on which it is possible to introduce a metric is called metrizable (cf. Metrizable space). A set
on which it is possible to introduce a metric is called metrizable (cf. Metrizable space). A set 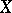 provided with a metric is called a metric space.
provided with a metric is called a metric space.
Examples.
1) On any set there is the discrete metric
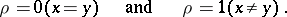 |
2) In the space  various metrics are possible, among them are:
various metrics are possible, among them are:
 |
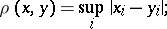 |
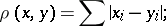 |
here 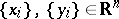 .
.
3) In a Riemannian space a metric is defined by a metric tensor, or a quadratic differential form (in some sense, this is an analogue of the first metric of example 2)). For a generalization of metrics of this type see Finsler space.
4) In function spaces on a (countably) compact space 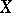 there are also various metrics; for example, the uniform metric
there are also various metrics; for example, the uniform metric
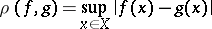 |
(an analogue of the second metric of example 2)), and the integral metric
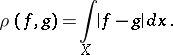 |
5) In normed spaces over 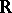 a metric is defined by the norm
a metric is defined by the norm  :
:
 |
6) In the space of closed subsets of a metric space there is the Hausdorff metric.
If, instead of 1), one requires only:
1')  if
if 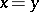 (so that from
(so that from 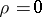 it does not always follows that
it does not always follows that  ), the function
), the function 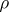 is called a pseudo-metric [2], [3], or finite écart [4].
is called a pseudo-metric [2], [3], or finite écart [4].
A metric (and even a pseudo-metric) makes the definition of a number of additional structures on the set 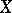 possible. First of all a topology (see Topological space), and in addition a uniformity (see Uniform space) or a proximity (see Proximity space) structure. The term metric is also used to denote more general notions which do not have all the properties 1)–3); such are, for example, an indefinite metric, a symmetry on a set, etc.
possible. First of all a topology (see Topological space), and in addition a uniformity (see Uniform space) or a proximity (see Proximity space) structure. The term metric is also used to denote more general notions which do not have all the properties 1)–3); such are, for example, an indefinite metric, a symmetry on a set, etc.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
| [2] | J.L. Kelley, "General topology" , Springer (1975) |
| [3] | K. Kuratowski, "Topology" , 1 , PWN & Acad. Press (1966) (Translated from French) |
| [4] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
Comments
Potentially, any metric space  has a second metric
has a second metric 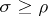 naturally associated: the intrinsic or internal metric. Potentially, because the definition may give
naturally associated: the intrinsic or internal metric. Potentially, because the definition may give  for some pairs of points
for some pairs of points  . One defines the length (which may be
. One defines the length (which may be  ) of a continuous path
) of a continuous path 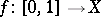 by
by  , where
, where  is the infimum of all finite sums
is the infimum of all finite sums 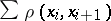 with
with 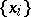 a finite subset of
a finite subset of 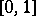 which is an
which is an  -net (cf. Metric space) and is listed in the natural order. Then
-net (cf. Metric space) and is listed in the natural order. Then 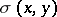 is the infimum of the lengths of paths
is the infimum of the lengths of paths 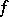 with
with 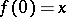 ,
,  , but
, but  if there is no such path of finite length.
if there is no such path of finite length.
No reasonable topological restriction on 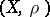 suffices to guarantee that the intrinsic "metric" (or écart)
suffices to guarantee that the intrinsic "metric" (or écart) 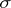 will be finite-valued. If
will be finite-valued. If 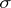 is finite-valued, suitable compactness conditions will assure that minimum-length paths, i.e. paths from
is finite-valued, suitable compactness conditions will assure that minimum-length paths, i.e. paths from  to
to 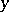 of length
of length 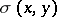 , exist. When every pair of points
, exist. When every pair of points 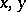 is joined by a path (non-unique, in general) of length
is joined by a path (non-unique, in general) of length 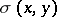 , the metric is often called convex. (This is much weaker than the surface theorists' convex metric.) The main theorem in this area is that every locally connected metric continuum admits a convex metric [a1], [a2].
, the metric is often called convex. (This is much weaker than the surface theorists' convex metric.) The main theorem in this area is that every locally connected metric continuum admits a convex metric [a1], [a2].
References
| [a1] | R.H. Bing, "Partitioning a set" Bull. Amer. Math. Soc. , 55 (1949) pp. 1101–1110 |
| [a2] | E.E. Moïse, "Grille decomposition and convexification" Bull. Amer. Math. Soc. , 55 (1949) pp. 1111–1121 |
Metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Metric&oldid=12195