Measurable flow
in a measure space 
A family  (
( runs over the set of real numbers
runs over the set of real numbers  ) of automorphisms of the space such that: 1)
) of automorphisms of the space such that: 1)  for all
for all  ,
,  ; and 2) the mapping
; and 2) the mapping  taking
taking 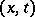 to
to 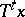 is measurable (a measure is introduced on
is measurable (a measure is introduced on 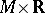 as the direct product of the measure
as the direct product of the measure 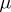 in
in  and the Lebesgue measure in
and the Lebesgue measure in 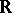 ). "Automorphisms" here are to be understood in the strict sense of the word (and not modulo 0), that is, the
). "Automorphisms" here are to be understood in the strict sense of the word (and not modulo 0), that is, the  must be bijections
must be bijections 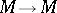 carrying measurable sets to measurable sets of the same measure. In using automorphisms modulo 0, it turns out to be expedient to replace condition 2) by a condition of a different character, which leads to the concept of a continuous flow. Measurable flows are used in ergodic theory.
carrying measurable sets to measurable sets of the same measure. In using automorphisms modulo 0, it turns out to be expedient to replace condition 2) by a condition of a different character, which leads to the concept of a continuous flow. Measurable flows are used in ergodic theory.
Measurable flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Measurable_flow&oldid=11332