Mean-value characterization
Harmonic functions.
Let 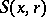 denote the sphere of radius
denote the sphere of radius  and centre
and centre  in
in  and let
and let 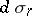 be the normalized Lebesgue measure on
be the normalized Lebesgue measure on 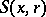 . One version of the classical converse of Gauss' mean-value theorem for harmonic functions asserts that a function
. One version of the classical converse of Gauss' mean-value theorem for harmonic functions asserts that a function 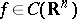 which satisfies
which satisfies
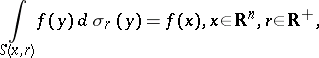 | (a1) |
is harmonic in  (cf. also Harmonic function). In fact, one need only require that (a1) holds for
(cf. also Harmonic function). In fact, one need only require that (a1) holds for 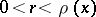 , where
, where 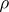 is an arbitrary positive function of
is an arbitrary positive function of  . A corresponding "local" result holds for continuous functions defined on an arbitrary domain in
. A corresponding "local" result holds for continuous functions defined on an arbitrary domain in 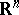 .
.
Remarkably, for the harmonicity of 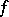 it suffices that (a1) holds only for two distinct values of
it suffices that (a1) holds only for two distinct values of  (and all
(and all  ), so long as the radii are not related in a special way. Specifically, let
), so long as the radii are not related in a special way. Specifically, let
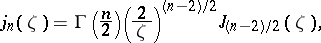 |
where 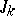 is the Bessel function of the first kind of order
is the Bessel function of the first kind of order 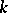 (cf. also Bessel functions), and let
(cf. also Bessel functions), and let 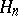 be the set of positive quotients of zeros of
be the set of positive quotients of zeros of 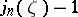 . J. Delsarte proved that if (a1) holds for
. J. Delsarte proved that if (a1) holds for 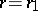 and
and 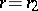 and
and 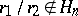 , then
, then 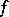 is harmonic in
is harmonic in 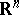 [a11], cf. [a20]. (In fact,
[a11], cf. [a20]. (In fact, 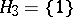 , so any two distinct radii are sufficient in dimension
, so any two distinct radii are sufficient in dimension  .) In [a10], Delsarte's theorem is extended to non-compact irreducible symmetric spaces of rank
.) In [a10], Delsarte's theorem is extended to non-compact irreducible symmetric spaces of rank 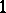 . There is also a local version of this result [a9], [a21]. Let
. There is also a local version of this result [a9], [a21]. Let 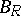 be the ball of radius
be the ball of radius 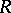 centred at
centred at  in
in 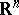 . Now, if
. Now, if 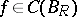 satisfies (a1) for
satisfies (a1) for 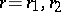 (
(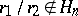 ) and
) and  such that
such that  , then
, then 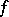 is harmonic on
is harmonic on 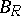 so long as
so long as 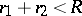 .
.
In this connection, one should also mention Littlewood's one-circle problem, solved by W. Hansen and N. Nadirashvili [a14]. Let 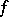 be a bounded continuous function on the open unit disc
be a bounded continuous function on the open unit disc 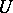 in
in 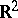 . Suppose that for each point in
. Suppose that for each point in 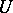 there exists an
there exists an 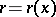 such that the mean-value condition of (a1) holds. Must
such that the mean-value condition of (a1) holds. Must 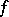 be harmonic? The answer turns out to be "no" [a14]. On the other hand, the one-radius condition obtained by replacing the peripheral mean in (a1) by the (areal) average over the disc of radius
be harmonic? The answer turns out to be "no" [a14]. On the other hand, the one-radius condition obtained by replacing the peripheral mean in (a1) by the (areal) average over the disc of radius 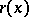 does imply harmonicity [a13]. This last result extends to functions defined on arbitrary bounded domains in
does imply harmonicity [a13]. This last result extends to functions defined on arbitrary bounded domains in 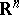 (and many unbounded domains as well); one can also weaken the boundedness assumption on
(and many unbounded domains as well); one can also weaken the boundedness assumption on 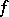 to
to 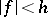 for some positive harmonic function
for some positive harmonic function 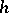 . For a survey of these and related results, see [a12].
. For a survey of these and related results, see [a12].
Interesting new phenomena arise when one allows the integration to extend over the full space on which 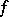 is defined. Consider, for instance, functions integrable with respect to the (normalized) Lebesgue measure
is defined. Consider, for instance, functions integrable with respect to the (normalized) Lebesgue measure 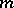 on the unit ball
on the unit ball 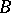 in
in 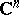 . If
. If 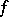 is harmonic with respect to the invariant Laplacian [a17], 4.1, then
is harmonic with respect to the invariant Laplacian [a17], 4.1, then
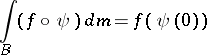 |
for every 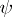 in
in 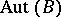 . The converse holds if and only if
. The converse holds if and only if 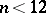 [a1], cf. [a7] and, for a Euclidean analogue, [a6]. Asymptotic mean-value conditions for (non-integrable) functions on
[a1], cf. [a7] and, for a Euclidean analogue, [a6]. Asymptotic mean-value conditions for (non-integrable) functions on  are studied in [a8]. Finally, for a detailed overview of the whole subject, see [a15].
are studied in [a8]. Finally, for a detailed overview of the whole subject, see [a15].
Generalization.
The extent to which mean-value theorems and their converses generalize to differential equations other than 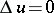 is explored in [a22]. There it is shown that if
is explored in [a22]. There it is shown that if 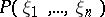 is a homogeneous polynomial, then
is a homogeneous polynomial, then  is a (weak) solution of the differential equation
is a (weak) solution of the differential equation 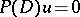 if and only if it satisfies the generalized mean-value condition
if and only if it satisfies the generalized mean-value condition
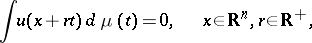 | (a2) |
where 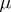 is an appropriate complex measure supported on the unit ball of
is an appropriate complex measure supported on the unit ball of 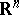 and
and 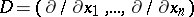 . (The choice
. (The choice 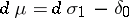 corresponds to (a1).) The local version of this result requires that (a2) holds for all
corresponds to (a1).) The local version of this result requires that (a2) holds for all 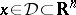 and all
and all 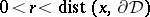 . Solutions of
. Solutions of 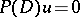 are also characterized by two-radius theorems of Delsarte type [a22], [a23], cf. [a19].
are also characterized by two-radius theorems of Delsarte type [a22], [a23], cf. [a19].
Pluriharmonic and separately harmonic functions.
Mean-value characterizations of pluriharmonic functions (i.e., real parts of holomorphic functions, cf. also Pluriharmonic function) and separately harmonic functions (i.e., functions harmonic with respect to each variable 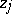 ,
, 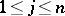 ) are studied in [a3]. Let
) are studied in [a3]. Let
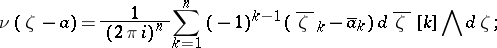 |
here 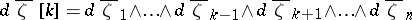 ,
, 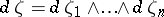 . If
. If 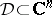 is a complete bounded Reinhardt domain with centre at the point
is a complete bounded Reinhardt domain with centre at the point  and
and  is separately harmonic in
is separately harmonic in 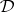 and continuous in
and continuous in 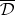 , then
, then
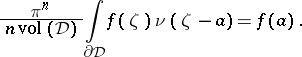 | (a3) |
Take for  the
the  -circular ellipsoids with centre at the point
-circular ellipsoids with centre at the point  ,
,
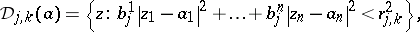 |
where 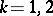 ,
, 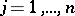 , and all
, and all 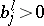 . Then the following result holds. Let
. Then the following result holds. Let 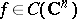 be such that for each
be such that for each 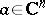 the
the 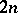 conditions obtained by setting in (a3)
conditions obtained by setting in (a3) 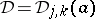 ,
, 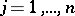 , and
, and 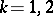 hold. If no
hold. If no 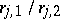 belongs to
belongs to 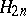 and if
and if
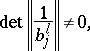 |
then 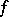 is separately harmonic in
is separately harmonic in 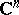 .
.
Similarly, if 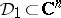 is a complete bounded circular (Cartan) domain with centre at the point
is a complete bounded circular (Cartan) domain with centre at the point  (cf. also Reinhardt domain) and
(cf. also Reinhardt domain) and 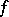 is pluriharmonic in
is pluriharmonic in 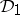 and continuous in
and continuous in 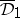 , then
, then
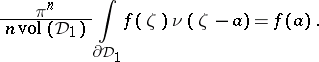 | (a4) |
Consider now circular ellipsoids with centre at the point  :
:
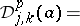 |
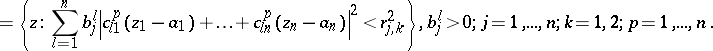 |
Let 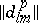 (
(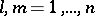 ) be the inverse matrix of
) be the inverse matrix of 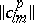 for
for 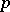 fixed. Let
fixed. Let 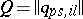 (
(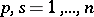 ;
; 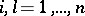 ) be the
) be the 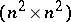 -matrix with entries
-matrix with entries
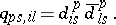 |
Then the following result holds. Let 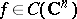 be such that for every
be such that for every 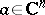 the conditions (a4) hold for
the conditions (a4) hold for 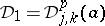 ,
, 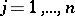 ,
, 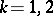 ,
, 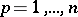 (
(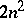 conditions). If
conditions). If 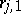 and
and 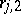 are such that no
are such that no 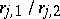 belongs to
belongs to 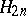 ,
, 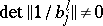 and
and 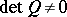 , then
, then 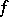 is pluriharmonic.
is pluriharmonic.
Local versions of the above-mentioned results are given also in [a3], as well as mean-value characterizations of pluriharmonic functions and separately harmonic functions by integration over the distinguished boundaries of poly-discs.
Holomorphic and pluriharmonic functions.
In certain situations, Temlyakov–Opial–Siciak-type mean-value theorems (see [a2], [a16], [a18]) can be used to characterize holomorphic and pluriharmonic functions. For 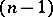 -times continuously differentiable functions
-times continuously differentiable functions 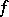 on
on 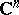 , the integral representation under discussion can be written as
, the integral representation under discussion can be written as
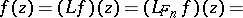 | (a5) |
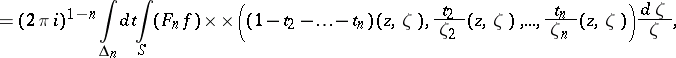 |
where 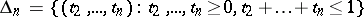 is the unit simplex in the real Euclidean
is the unit simplex in the real Euclidean 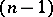 -dimensional space,
-dimensional space,  ,
, 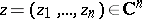 ,
, 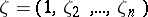 ,
, 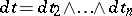 ,
, 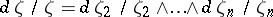 , and
, and 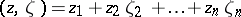 . Let
. Let 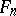 denote a certain differential operator of order
denote a certain differential operator of order 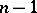 , which will be specified separately for holomorphic functions, for pluriharmonic functions, and also for anti-holomorphic functions (that is, functions holomorphic with respect to
, which will be specified separately for holomorphic functions, for pluriharmonic functions, and also for anti-holomorphic functions (that is, functions holomorphic with respect to 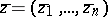 ). More precisely,
). More precisely,
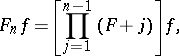 |
with the first-order differential operator to be specified, as mentioned above.
In [a4], the following criteria are proved for functions that are 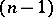 -times continuously differentiable on
-times continuously differentiable on 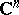 .
.
A function 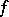 is holomorphic in
is holomorphic in 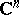 if and only if (a5) holds with
if and only if (a5) holds with
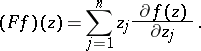 |
A function 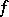 is anti-holomorphic on
is anti-holomorphic on 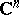 if and only if (a5) holds with
if and only if (a5) holds with
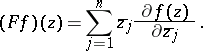 |
A function 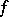 is pluriharmonic on
is pluriharmonic on 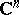 if and only if (a5) holds with
if and only if (a5) holds with
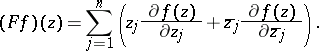 |
These results remain true without the assumption of smoothness; in this case, derivatives being understood in the distributional sense [a5].
References
| [a1] | P. Ahern, M. Flores, W. Rudin, "An invariant volume-mean-value property" J. Funct. Anal. , 11 (1993) pp. 380–397 |
| [a2] | L.A. Aizenberg, "Pluriharmonic functions" Dokl. Akad. Nauk. SSSR , 124 (1959) pp. 967–969 (In Russian) |
| [a3] | L.A. Aizenberg, C.A. Berenstein, L. Wertheim, "Mean-value characterization of pluriharmonic and separately harmonic functions" Pacific J. Math. , 175 (1996) pp. 295–306 |
| [a4] | L. Aizenberg, E. Liflyand, "Mean-value characterization of holomorphic and pluriharmonic functions" Complex Variables , 32 (1997) pp. 131–146 |
| [a5] | L. Aizenberg, E. Liflyand, "Mean-value characterization of holomorphic and pluriharmonic functions, II" Complex Variables , 39 (1999) pp. 381–390 |
| [a6] | Y. Ben Natan, Y. Weit, "Integrable harmonic functions on 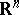 " J. Funct. Anal. , 150 (1997) pp. 471–477 " J. Funct. Anal. , 150 (1997) pp. 471–477 |
| [a7] | Y. Ben Natan, Y. Weit, "Integrable harmonic functions and symmetric spaces of rank one" J. Funct. Anal. , 160 (1998) pp. 141–149 |
| [a8] | Y. Benyamini, Y. Weit, "Functions satisfying the mean value property in the limit" J. Anal. Math. , 52 (1989) pp. 167–198 |
| [a9] | C.A. Berenstein, R. Gay, "A local version of the two-circles theorem" Israel J. Math. , 55 (1986) pp. 267–288 |
| [a10] | C.A. Berenstein, L. Zalcman, "Pompeiu's problem on symmetric spaces" Comment. Math. Helv. , 55 (1980) pp. 593–621 |
| [a11] | J. Delsarte, "Lectures on topics in mean periodic functions and the two-radius theorem" , Tata Institute, Bombay (1961) |
| [a12] | W. Hansen, "Restricted mean value property and harmonic functions" J. Kral (ed.) et al. (ed.) , Potential Theory–ICPT 94 (Proc. Intern. Conf., Konty) , de Gruyter (1996) pp. 67–90 |
| [a13] | W. Hansen, N. Nadirashvili, "A converse to the mean value theorem for harmonic functions" Acta Math. , 171 (1993) pp. 139–163 |
| [a14] | W. Hansen, N. Nadirashvili, "Littlewood's one circle problem" J. London Math. Soc. , 50 (1994) pp. 349–360 |
| [a15] | I. Netuka, J. Vesely, "Mean value property and harmonic functions" K. GowriSankaran (ed.) et al. (ed.) , Classical and Modern Potential Theory and Applications , Kluwer Acad. Publ. (1994) pp. 359–398 |
| [a16] | Z. Opial, J. Siciak, "Integral formulas for function holomorphic in convex  circular domains" Zeszyty Nauk. Uniw. Jagiello. Prace Mat. , 9 (1963) pp. 67–75 circular domains" Zeszyty Nauk. Uniw. Jagiello. Prace Mat. , 9 (1963) pp. 67–75 |
| [a17] | W. Rudin, "Function theory in the unit ball of 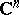 " , Springer (1980) " , Springer (1980) |
| [a18] | A.A. Temlyakov, "Integral representation of functions of two complex variables" Izv. Akad. Nauk. SSSR Ser. Mat. , 21 (1957) pp. 89–92 (In Russian) |
| [a19] | V.V. Volchkov, "New theorems on the mean for solutions of the Helmholtz equation" Russian Acad. Sci. Sb. Math. , 79 (1994) pp. 281–286 |
| [a20] | V.V. Volchkov, "New two-radii theorems in the theory of harmonic functions" Russian Acad. Sci. Izv. Math. , 44 (1995) pp. 181–192 |
| [a21] | V.V. Volchkov, "The final version of the mean value theorem for harmonic functions" Math. Notes , 59 (1996) pp. 247–252 |
| [a22] | L. Zalcman, "Offbeat integral geometry" Amer. Math. Monthly , 87 (1980) pp. 161–175 |
| [a23] | L. Zalcman, "Mean values and differential equations" Israel J. Math. , 14 (1973) pp. 339–352 |
Mean-value characterization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mean-value_characterization&oldid=14590