Difference between revisions of "Maximal ergodic theorem"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(refs format) |
||
| Line 11: | Line 11: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062950/m0629507.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062950/m0629507.png" /></td> </tr></table> | ||
| − | The maximal ergodic theorem is due to K. Yosida and S. Kakutani | + | The maximal ergodic theorem is due to K. Yosida and S. Kakutani {{Cite|YK}}, who showed that it can play a central role in the proof of the [[Birkhoff ergodic theorem|Birkhoff ergodic theorem]] (G.D. Birkhoff himself, instead of the maximal ergodic theorem, used somewhat different arguments). In later proofs of generalizations of Birkhoff's theorem (and also in related questions on the decomposition of the phase space into conservative and dissipative parts under conditions such that these generalizations make sense) a generalized maximal ergodic theorem is used in a similar way. There is a generalization of the maximal ergodic theorem due to E. Hopf and a simple proof of this generalization was given by A. García (see {{Cite|N}}). See also {{Cite|VY}} and the references in [[Birkhoff ergodic theorem|Birkhoff ergodic theorem]]. |
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|YK}}|| K. Yosida, S. Kakutani, "Birkhoff's ergodic theorem and the maximal ergodic theorem" ''Proc. Imp. Acad. Tokyo'' , '''15''' (1939) pp. 165–168 {{MR|355}} {{ZBL|}} | |
| − | + | |- | |
| + | |valign="top"|{{Ref|N}}|| J. Neveu, "Mathematical foundations of the calculus of probability" , Holden-Day (1965) (Translated from French) {{MR|0198505}} {{ZBL|0137.11301}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|VY}}|| A.M. Vershik, S.A. Yuzvinskii, "Dynamical systems with invariant measure" ''Progress in Math.'' , '''8''' (1970) pp. 151–215 ''Itogi Nauk. Anal.'' (1967) pp. 133–187 {{MR|0286981}} {{ZBL|0252.28006}} | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
| − | A variety of ergodic theorems (including historical remarks) can be found in | + | A variety of ergodic theorems (including historical remarks) can be found in {{Cite|K}}. |
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|K}}|| U. Krengel, "Ergodic theorems" , de Gruyter (1985) {{MR|0797411}} {{ZBL|0575.28009}} | ||
| + | |} | ||
Revision as of 19:24, 14 May 2012
2020 Mathematics Subject Classification: Primary: 37A30 [MSN][ZBL]
If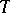 
is an endomorphism of a measure space 
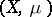, if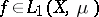 
and if 
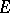is the set of 
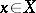for which
 |
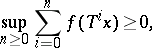then
 |
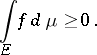The maximal ergodic theorem is due to K. Yosida and S. Kakutani [YK], who showed that it can play a central role in the proof of the Birkhoff ergodic theorem (G.D. Birkhoff himself, instead of the maximal ergodic theorem, used somewhat different arguments). In later proofs of generalizations of Birkhoff's theorem (and also in related questions on the decomposition of the phase space into conservative and dissipative parts under conditions such that these generalizations make sense) a generalized maximal ergodic theorem is used in a similar way. There is a generalization of the maximal ergodic theorem due to E. Hopf and a simple proof of this generalization was given by A. García (see [N]). See also [VY] and the references in Birkhoff ergodic theorem.
References
| [YK] | K. Yosida, S. Kakutani, "Birkhoff's ergodic theorem and the maximal ergodic theorem" Proc. Imp. Acad. Tokyo , 15 (1939) pp. 165–168 MR355 |
| [N] | J. Neveu, "Mathematical foundations of the calculus of probability" , Holden-Day (1965) (Translated from French) MR0198505 Zbl 0137.11301 |
| [VY] | A.M. Vershik, S.A. Yuzvinskii, "Dynamical systems with invariant measure" Progress in Math. , 8 (1970) pp. 151–215 Itogi Nauk. Anal. (1967) pp. 133–187 MR0286981 Zbl 0252.28006 |
Comments
A variety of ergodic theorems (including historical remarks) can be found in [K].
References
| [K] | U. Krengel, "Ergodic theorems" , de Gruyter (1985) MR0797411 Zbl 0575.28009 |
How to Cite This Entry:
Maximal ergodic theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_ergodic_theorem&oldid=23632
Maximal ergodic theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_ergodic_theorem&oldid=23632
This article was adapted from an original article by D.V. Anosov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article