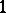Matrix
A rectangular array
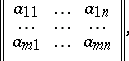 | (1) |
consisting of 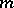 rows and
rows and  columns, the entries
columns, the entries 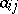 of which belong to some set
of which belong to some set 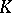 . (1) is called also an
. (1) is called also an  -dimensional matrix over
-dimensional matrix over 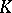 , or a matrix of dimensions
, or a matrix of dimensions 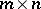 over
over 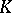 . Let
. Let 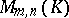 denote the set of all
denote the set of all  -dimensional matrices over
-dimensional matrices over 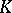 . If
. If  , then (1) is called a square matrix of order
, then (1) is called a square matrix of order  . The set of all square matrices of order
. The set of all square matrices of order  over
over 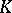 is denoted by
is denoted by 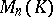 .
.
Alternative notations for matrices are:
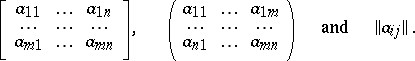 |
In the most important cases the role of 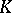 is played by the field of real numbers, the field of complex numbers, an arbitrary field, a ring of polynomials, the ring of integers, a ring of functions, or an arbitrary associative ring. The operations of addition and multiplication defined on
is played by the field of real numbers, the field of complex numbers, an arbitrary field, a ring of polynomials, the ring of integers, a ring of functions, or an arbitrary associative ring. The operations of addition and multiplication defined on 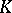 are carried over naturally to matrices over
are carried over naturally to matrices over 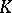 , and in this way one is led to the matrix calculus — the subject matter of the theory of matrices.
, and in this way one is led to the matrix calculus — the subject matter of the theory of matrices.
The notion of a matrix arose first in the middle of the 19th century in the investigations of W. Hamilton, and A. Cayley. Fundamental results in the theory of matrices are due to K. Weierstrass, C. Jordan and G. Frobenius. I.A. Lappo-Danilevskii has developed the theory of analytic functions of several matrix variables and has applied it to the study of systems of linear differential equations.
Operations with matrices.
Let 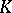 be an associative ring and let
be an associative ring and let 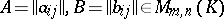 . Then the sum of the matrices
. Then the sum of the matrices 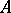 and
and 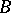 is, by definition,
is, by definition,
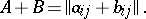 |
Clearly, 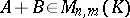 and addition of matrices is associative and commutative. The null matrix in
and addition of matrices is associative and commutative. The null matrix in 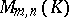 is the matrix 0, all entries of which are zero. For every
is the matrix 0, all entries of which are zero. For every 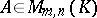 ,
,
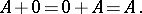 |
Let 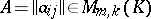 and
and 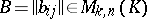 . The product of the two matrices
. The product of the two matrices 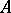 and
and 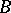 is defined by the rule
is defined by the rule
 |
where
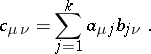 |
The product of two elements of 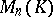 is always defined and belongs to
is always defined and belongs to 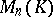 . Multiplication of matrices is associative: If
. Multiplication of matrices is associative: If 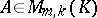 ,
, 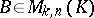 and
and 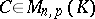 , then
, then
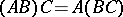 |
and 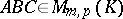 . The distributivity rule also holds: For
. The distributivity rule also holds: For 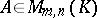 and
and 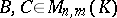 ,
,
 | (2) |
In particular, (2) holds also for 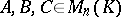 . Consequently,
. Consequently, 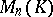 is an associative ring. If
is an associative ring. If 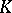 is a ring with an identity, then the matrix
is a ring with an identity, then the matrix
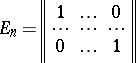 |
is the identity of the ring 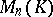 :
:
 |
for all 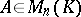 . Multiplication of matrices is not commutative: If
. Multiplication of matrices is not commutative: If 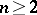 , for every associative ring
, for every associative ring 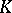 with an identity there are matrices
with an identity there are matrices 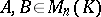 such that
such that 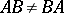 .
.
Let 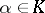 ,
, 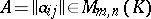 ; the product of the matrix
; the product of the matrix 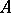 by the element (number, scalar)
by the element (number, scalar) 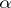 is, by definition, the matrix
is, by definition, the matrix 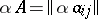 . Then
. Then
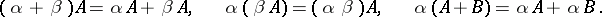 |
Let  be a ring with an identity. The matrix
be a ring with an identity. The matrix  is defined as the element of
is defined as the element of 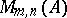 the only non-zero entry of which is the entry
the only non-zero entry of which is the entry 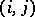 , which equals 1,
, which equals 1, 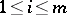 ,
, 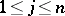 . For every
. For every 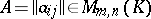 ,
,
 |
If 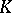 is a field, then
is a field, then 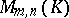 is an
is an 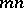 -dimensional vector space over
-dimensional vector space over 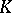 , and the matrices
, and the matrices  form a basis in this space.
form a basis in this space.
Block matrices.
Let 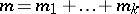 ,
, 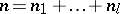 , where
, where 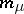 and
and 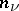 are positive integers. Then a matrix
are positive integers. Then a matrix 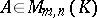 can be written in the form
can be written in the form
 | (3) |
where 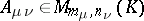 ,
, 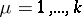 ,
, 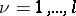 . The matrix (3) is called a block matrix. If
. The matrix (3) is called a block matrix. If 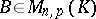 ,
, 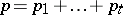 ,
, 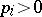 , and
, and 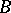 is written in the form
is written in the form
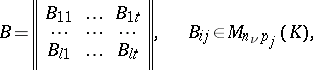 |
then
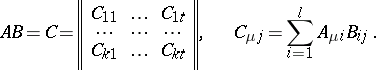 |
For example, if 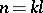 , then
, then  may be regarded as
may be regarded as  , where
, where 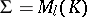 .
.
The matrix 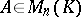 of the form
of the form
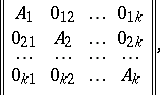 |
where 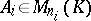 and
and 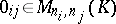 is the null matrix, is denoted by
is the null matrix, is denoted by 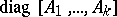 and is called block diagonal. The following holds:
and is called block diagonal. The following holds:
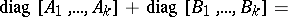 |
 |
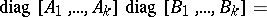 |
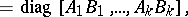 |
provided that the orders of 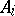 and
and 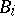 coincide for
coincide for 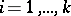 .
.
Square matrices over a field.
Let 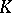 be a field, let
be a field, let 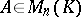 and let
and let 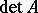 be the determinant of the matrix
be the determinant of the matrix 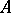 .
. 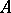 is said to be non-degenerate (or non-singular) if
is said to be non-degenerate (or non-singular) if 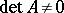 . A matrix
. A matrix 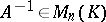 is called the inverse of
is called the inverse of 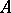 if
if 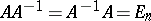 . The invertibility of
. The invertibility of 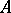 in
in 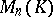 is equivalent to its non-degeneracy, and
is equivalent to its non-degeneracy, and
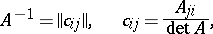 |
where 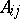 is the cofactor of the entry
is the cofactor of the entry 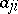 ,
,  . For
. For 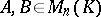 ,
,
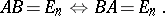 |
The set of all invertible elements of 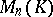 is a group under multiplication, called the general linear group and denoted by
is a group under multiplication, called the general linear group and denoted by 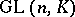 . The powers of a matrix
. The powers of a matrix 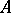 are defined as follows
are defined as follows
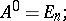 |
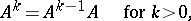 |
and if 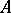 is invertible, then
is invertible, then 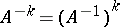 . For the polynomial
. For the polynomial
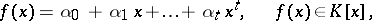 |
the matrix polynomial
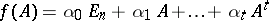 |
is defined.
Every matrix from 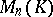 gives rise to a linear transformation of the
gives rise to a linear transformation of the  -dimensional vector space
-dimensional vector space 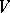 over
over 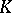 . Let
. Let  be a basis in
be a basis in 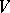 and let
and let 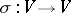 be a linear transformation of
be a linear transformation of 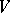 . Then
. Then  is uniquely determined by the set of vectors
is uniquely determined by the set of vectors
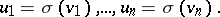 |
Moreover,
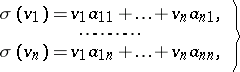 | (4) |
where 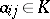 . The matrix
. The matrix 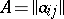 is called the matrix of the transformation
is called the matrix of the transformation 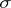 in the basis
in the basis  . For a fixed basis, the matrix
. For a fixed basis, the matrix 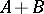 is the matrix of the linear transformation
is the matrix of the linear transformation 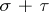 , while
, while 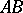 is the matrix of
is the matrix of  if
if 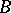 is the matrix of the linear transformation
is the matrix of the linear transformation  . Equality (4) may be written in the form
. Equality (4) may be written in the form
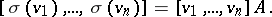 |
Suppose that  is a second basis in
is a second basis in 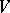 . Then
. Then 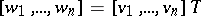 ,
, 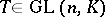 , and
, and 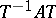 is the matrix of the transformation
is the matrix of the transformation 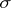 in the basis
in the basis  . Two matrices
. Two matrices 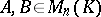 are similar if there is a matrix
are similar if there is a matrix 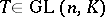 such that
such that 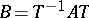 . Here, also,
. Here, also,  and the ranks of the matrices
and the ranks of the matrices 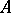 and
and 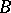 coincide. The linear transformation
coincide. The linear transformation 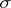 is called non-degenerate, or non-singular, if
is called non-degenerate, or non-singular, if  ;
; 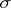 is non-degenerate if and only if its matrix is non-degenerate. If
is non-degenerate if and only if its matrix is non-degenerate. If 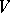 is regarded as the space of columns
is regarded as the space of columns 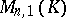 , then every linear transformation in
, then every linear transformation in 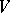 is given by left multiplication of the columns
is given by left multiplication of the columns 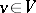 by some
by some  :
: 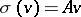 , and the matrix of
, and the matrix of 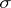 in the basis
in the basis
 |
coincides with  . A matrix
. A matrix 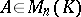 is singular (or degenerate) if and only if there is a column
is singular (or degenerate) if and only if there is a column 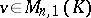 ,
, 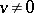 , such that
, such that 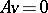 .
.
Transposition and matrices of special form.
Let  . Then the matrix
. Then the matrix 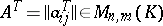 , where
, where 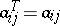 , is called the transpose of
, is called the transpose of 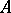 . Alternative notations are
. Alternative notations are 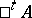 and
and 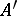 . Let
. Let 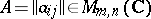 . Then
. Then 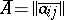 , where
, where 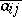 is the complex conjugate of the number
is the complex conjugate of the number 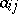 , is called the complex conjugate of
, is called the complex conjugate of 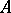 . The matrix
. The matrix  , where
, where 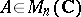 , is called the Hermitian conjugate of
, is called the Hermitian conjugate of 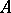 . Many matrices used in applications are given special names:'
. Many matrices used in applications are given special names:'
<tbody> </tbody>
|
Polynomial matrices.
Let 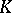 be a field and let
be a field and let 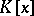 be the ring of all polynomials in the variable
be the ring of all polynomials in the variable  with coefficients from
with coefficients from  . A matrix over
. A matrix over 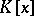 is called a polynomial matrix. For the elements of the ring
is called a polynomial matrix. For the elements of the ring  one introduces the following elementary operations: 1) multiplication of a row or column of a matrix by a non-zero element of the field
one introduces the following elementary operations: 1) multiplication of a row or column of a matrix by a non-zero element of the field 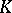 ; and 2) addition to a row (column) of another row (respectively, column) of the given matrix, multiplied by a polynomial from
; and 2) addition to a row (column) of another row (respectively, column) of the given matrix, multiplied by a polynomial from 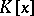 . Two matrices
. Two matrices 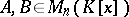 are called equivalent
are called equivalent 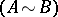 if
if 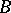 can be obtained from
can be obtained from 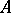 through a finite number of elementary operations.
through a finite number of elementary operations.
Let
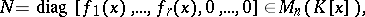 |
where a) 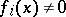 ; b)
; b) 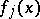 is divisible by
is divisible by 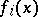 for
for 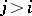 ; and c) the coefficient of the leading term in
; and c) the coefficient of the leading term in  is equal to 1. Then
is equal to 1. Then 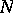 is called a canonical polynomial matrix. Every equivalence class of elements of the ring
is called a canonical polynomial matrix. Every equivalence class of elements of the ring 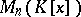 contains a unique canonical matrix. If
contains a unique canonical matrix. If  , where
, where
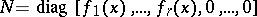 |
is a canonical matrix, then the polynomials
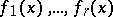 |
are called the invariant factors of 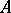 ; the number
; the number  is identical with the rank of
is identical with the rank of 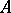 . A matrix
. A matrix 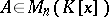 has an inverse in
has an inverse in 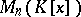 if and only if
if and only if 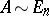 . The last condition is in turn equivalent to
. The last condition is in turn equivalent to  . Two matrices
. Two matrices 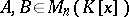 are equivalent if and only if
are equivalent if and only if
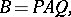 |
where 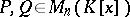 ,
, 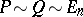 .
.
Let  . The matrix
. The matrix
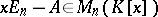 |
is called the characteristic matrix of  and
and 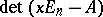 is called the characteristic polynomial of
is called the characteristic polynomial of 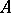 . For every polynomial of the form
. For every polynomial of the form
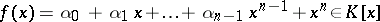 |
there is an 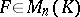 such that
such that
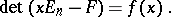 |
Such is, for example, the matrix
 | (*) |
The characteristic polynomials of two similar matrices coincide. However, the fact that two matrices have identical characteristic polynomials does not necessarily entail the fact that the matrices are similar. A similarity criterion is: Two matrices 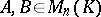 are similar if and only if the polynomial matrices
are similar if and only if the polynomial matrices 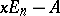 and
and 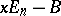 are equivalent. The set of all matrices from
are equivalent. The set of all matrices from 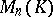 having a given characteristic polynomial
having a given characteristic polynomial 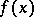 is partitioned into a finite number of classes of similar matrices; this set reduces to a single class if and only if
is partitioned into a finite number of classes of similar matrices; this set reduces to a single class if and only if 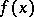 does not have multiple factors in
does not have multiple factors in  .
.
Let 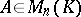 ,
, 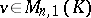 ,
, 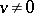 , and suppose that
, and suppose that  , where
, where 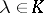 . Then
. Then  is called an eigen vector of
is called an eigen vector of 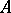 and
and 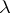 is called an eigen value of
is called an eigen value of 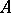 . An element
. An element 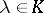 is an eigen value of a matrix
is an eigen value of a matrix 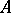 if and only if it is a root of the characteristic polynomial of
if and only if it is a root of the characteristic polynomial of 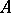 . The set of all columns
. The set of all columns 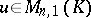 such that
such that 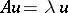 for a fixed eigen value
for a fixed eigen value 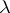 of
of 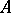 is a subspace of
is a subspace of 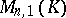 . The dimension of this subspace equals the defect (or deficiency)
. The dimension of this subspace equals the defect (or deficiency) 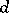 of the matrix
of the matrix 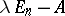 (
( , where
, where  is the rank of
is the rank of 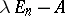 ). The number
). The number 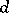 does not exceed the multiplicity of the root
does not exceed the multiplicity of the root 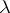 , but need not coincide with it. A matrix
, but need not coincide with it. A matrix 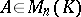 is similar to a diagonal matrix if and only if it has
is similar to a diagonal matrix if and only if it has  linearly independent eigen vectors. If for an
linearly independent eigen vectors. If for an 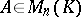 ,
,
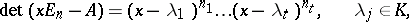 |
and the roots 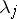 are distinct, then the following holds:
are distinct, then the following holds: 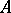 is similar to a diagonal matrix if and only if for each
is similar to a diagonal matrix if and only if for each 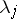 ,
, 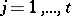 , the defect of
, the defect of 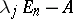 coincides with
coincides with 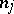 . In particular, every matrix with
. In particular, every matrix with  distinct eigen values is similar to a diagonal matrix. Over an algebraically closed field every matrix from
distinct eigen values is similar to a diagonal matrix. Over an algebraically closed field every matrix from 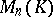 is similar to some triangular matrix from
is similar to some triangular matrix from 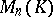 . The Hamilton–Cayley theorem: If
. The Hamilton–Cayley theorem: If 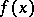 is the characteristic polynomial of a matrix
is the characteristic polynomial of a matrix 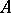 , then
, then 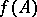 is the null matrix.
is the null matrix.
By definition, the minimum polynomial of a matrix 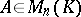 is the polynomial
is the polynomial 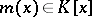 with the properties:
with the properties: 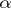 )
) 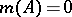 ;
; 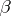 ) the coefficient of the leading term equals 1; and
) the coefficient of the leading term equals 1; and 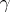 ) if
) if 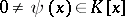 and the degree of
and the degree of 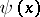 is smaller than the degree of
is smaller than the degree of  , then
, then 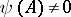 . Every matrix has a unique minimum polynomial. If
. Every matrix has a unique minimum polynomial. If 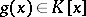 and
and 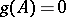 , then the minimum polynomial
, then the minimum polynomial 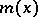 of
of 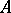 divides
divides 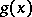 . The minimum polynomial and the characteristic polynomial of
. The minimum polynomial and the characteristic polynomial of 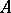 coincide with the last invariant factor, and, respectively, the product of all invariant factors, of the matrix
coincide with the last invariant factor, and, respectively, the product of all invariant factors, of the matrix 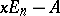 . The minimum polynomial of
. The minimum polynomial of 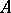 equals
equals
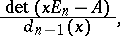 |
where  is the greatest common divisor of the minors (cf. Minor) of order
is the greatest common divisor of the minors (cf. Minor) of order 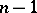 of the matrix
of the matrix 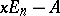 . A matrix
. A matrix 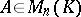 is similar to a diagonal matrix over the field
is similar to a diagonal matrix over the field 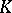 if and only if its minimum polynomial is a product of distinct linear factors in the ring
if and only if its minimum polynomial is a product of distinct linear factors in the ring 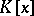 .
.
A matrix 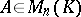 is called nilpotent if
is called nilpotent if 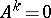 for some integer
for some integer 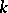 . A matrix
. A matrix 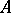 is nilpotent if and only if
is nilpotent if and only if  . Every nilpotent matrix from
. Every nilpotent matrix from 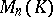 is similar to some triangular matrix with zeros on the diagonal.
is similar to some triangular matrix with zeros on the diagonal.
References
| [1] | V.V. Voevodin, "Algèbre linéare" , MIR (1976) (Translated from Russian) |
| [2] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) |
| [3] | A.I. Kostrikin, "Introduction to algebra" , Springer (1982) (Translated from Russian) |
| [4] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
| [5] | A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian) |
| [6] | I.B. Proskuryakov, "Higher algebra. Linear algebra, polynomials, general algebra" , Pergamon (1965) (Translated from Russian) |
| [7] | A.R.I. Tyshkevich, "Linear algebra and analytic geometry" , Minsk (1976) (In Russian) |
| [8] | R. Bellman, "Introduction to matrix analysis" , McGraw-Hill (1970) |
| [9] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [10] | P. Lancaster, "Theory of matrices" , Acad. Press (1969) |
| [11] | M. Marcus, H. Minc, "A survey of matrix theory and matrix inequalities" , Allyn & Bacon (1964) |
Comments
The result on canonical polynomial matrices quoted above has a natural generalization to matrices over principal ideal domains. An 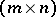 -matrix
-matrix 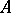 over a principal ideal domain
over a principal ideal domain 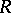 of the form
of the form
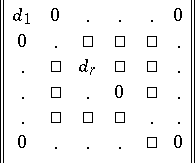 | (a1) |
with 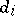 divisible by
divisible by 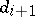 ,
, 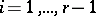 , is said to be in Smith canonical form. Every matrix
, is said to be in Smith canonical form. Every matrix 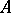 over a principal ideal domain
over a principal ideal domain 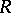 is equivalent to one in Smith canonical form in the sense that there are an
is equivalent to one in Smith canonical form in the sense that there are an 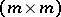 -matrix
-matrix 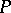 and an
and an 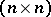 -matrix
-matrix 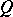 such that
such that 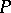 and
and 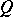 are invertible in
are invertible in 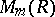 and
and 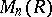 , respectively, and such that
, respectively, and such that 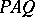 is in Smith canonical form.
is in Smith canonical form.
A matrix of the form (a1) is said to be in companion form, especially in linear systems and control theory where the theory of (polynomial) matrices finds many applications.
References
| [a1] | P.M. Cohn, "Algebra" , 1 , Wiley (1974) pp. Sect. 10.6 |
| [a2] | W.A. Wolovich, "Linear multivariable systems" , Springer (1974) |
| [a3] | R.E. Kalman, P.L. Falb, M.A. Arbib, "Topics in mathematical systems theory" , Prentice-Hall (1969) |
Matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix&oldid=17958
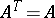
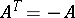
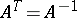
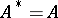
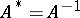
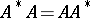
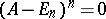
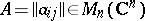 ,
,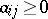 ,
,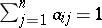 ,
, 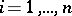
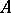 and
and 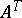 are stochastic
are stochastic -matrix
-matrix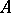 is either
is either  or
or