Mapping-cone construction
The construction that associates with every continuous mapping  of topological spaces the topological space
of topological spaces the topological space  obtained from the topological sum (disjoint union)
obtained from the topological sum (disjoint union)  (here
(here  is the cone over
is the cone over  ) by identifying
) by identifying  ,
,  . The space
. The space  is called the mapping cone of
is called the mapping cone of  . If
. If 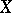 and
and  are pointed spaces with distinguished points
are pointed spaces with distinguished points 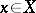 ,
, 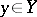 , then the generator
, then the generator 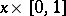 of
of  is contracted to a point, and
is contracted to a point, and 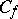 is said to be the collapsed mapping cone of
is said to be the collapsed mapping cone of 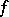 . For an arbitrary pointed topological space
. For an arbitrary pointed topological space 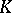 , the sequence
, the sequence 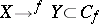 induces an exact sequence
induces an exact sequence
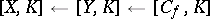 |
of pointed sets. The mapping 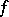 is homotopic to the constant mapping to the distinguished point if and only if
is homotopic to the constant mapping to the distinguished point if and only if 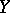 is a retract of
is a retract of  (cf. Retract of a topological space).
(cf. Retract of a topological space).
References
| [1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [2] | M.K. Tangora, "Cohomology operations and their applications in homotopy theory" , Harper & Row (1968) |
Comments
The algebraic analogue of the mapping-cone construction is as follows.
Let 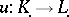 be a morphism of complexes, i.e.
be a morphism of complexes, i.e. 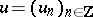 and
and 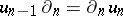 , where
, where 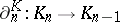 . The mapping cone of
. The mapping cone of  is the complex
is the complex 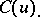 defined by
defined by
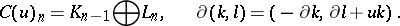 |
The injections 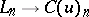 define a morphism of complexes and if
define a morphism of complexes and if 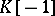 denotes the complex with
denotes the complex with  and
and 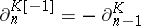 , then the projections
, then the projections 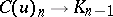 yield
yield
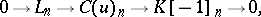 |
which fit together to define a short exact sequence of complexes
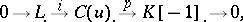 |
and there results a long exact homology sequence
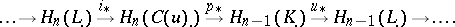 |
By turning a complex 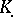 into a "co-complex"
into a "co-complex"  ,
, 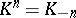 , the analogous constructions and results in a cohomological setting are obtained.
, the analogous constructions and results in a cohomological setting are obtained.
The complex 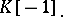 is called the suspension of the complex
is called the suspension of the complex 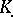 .
.
References
| [a1] | S. MacLane, "Homology" , Springer (1963) pp. Sect. II.4 |
Mapping-cone construction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mapping-cone_construction&oldid=19101