Mapping
single-valued
A law according to which to every element of a given set 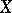 has been assigned a completely defined element of another given set
has been assigned a completely defined element of another given set 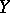 (
(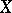 may coincide with
may coincide with 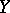 ). Such a relation between the elements
). Such a relation between the elements 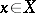 and
and 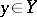 is denoted in the form
is denoted in the form 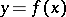 ,
, 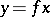 or
or 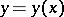 . One also writes
. One also writes 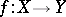 and says that the mapping
and says that the mapping 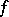 operates from
operates from 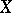 into
into  . The set
. The set 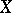 is called the domain (of definition) of the mapping, while the set
is called the domain (of definition) of the mapping, while the set 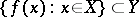 is called the range (of values) of the mapping. The mapping
is called the range (of values) of the mapping. The mapping 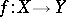 is also called a mapping of the set
is also called a mapping of the set 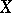 into the set
into the set 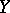 (or onto the set
(or onto the set 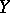 if
if 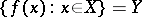 ). Logically, the concept of a "mapping" coincides with the concept of a function, an operator or a transformation.
). Logically, the concept of a "mapping" coincides with the concept of a function, an operator or a transformation.
A mapping 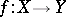 gives rise to a set
gives rise to a set 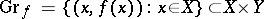 , which is called the graph of the mapping. On the other hand, a set
, which is called the graph of the mapping. On the other hand, a set 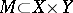 defines a single-valued mapping
defines a single-valued mapping 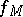 having graph
having graph 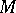 if and only if for all
if and only if for all 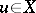 one and only one
one and only one 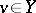 exists such that
exists such that 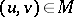 ; and then
; and then 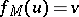 .
.
Two mappings 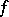 and
and 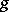 are said to be equal if their domains of definition coincide and if
are said to be equal if their domains of definition coincide and if 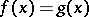 for each
for each 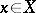 . In this case the ranges of these mappings also coincide. A mapping
. In this case the ranges of these mappings also coincide. A mapping 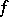 defined on
defined on 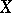 is constant if there is an
is constant if there is an  such that
such that 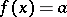 for every
for every  . The mapping
. The mapping 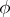 defined on a subset
defined on a subset 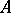 of
of 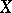 by the equality
by the equality 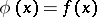 ,
, 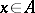 , is called the restriction of the mapping
, is called the restriction of the mapping 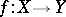 to
to 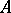 ; this restriction is often denoted by
; this restriction is often denoted by 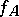 . A mapping
. A mapping 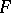 defined on a set
defined on a set 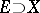 and satisfying the equality
and satisfying the equality  for all
for all 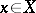 is called an extension (or continuation) of the mapping to
is called an extension (or continuation) of the mapping to 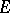 . If three sets
. If three sets  are given, if a mapping
are given, if a mapping  with values in
with values in 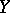 is defined on
is defined on  , and a mapping
, and a mapping 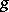 with values in
with values in 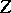 is defined on
is defined on 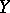 , then there exists a mapping
, then there exists a mapping 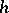 with domain of definition
with domain of definition 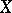 , taking values in
, taking values in  , and defined by the equality
, and defined by the equality 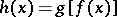 . This mapping is called the composite of the mappings
. This mapping is called the composite of the mappings 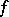 and
and 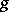 , while
, while 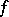 and
and 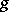 are called component (factor) mappings. The mapping
are called component (factor) mappings. The mapping 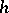 is also called the compound mapping (composite mapping, composed mapping), consisting of the interior mapping
is also called the compound mapping (composite mapping, composed mapping), consisting of the interior mapping 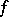 and the exterior mapping
and the exterior mapping 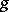 . The composed mapping is denoted by
. The composed mapping is denoted by 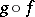 , where the order of the notation is vital (for functions of a real variable, the term superposition is also used). The concept of a compound mapping can be generalized to any finite number of components of the mapping.
, where the order of the notation is vital (for functions of a real variable, the term superposition is also used). The concept of a compound mapping can be generalized to any finite number of components of the mapping.
A mapping 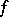 , defined on
, defined on 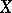 and taking values in
and taking values in 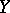 , gives rise to a new mapping defined on the subsets of
, gives rise to a new mapping defined on the subsets of 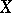 and taking subsets of
and taking subsets of 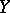 as values. In fact, if
as values. In fact, if 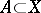 , then
, then
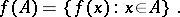 |
The set 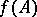 is called the image of
is called the image of 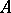 . If
. If 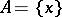 , the initial mapping
, the initial mapping 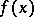 is obtained; thus,
is obtained; thus, 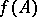 is an extension of
is an extension of 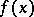 from the set
from the set 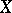 to the set
to the set 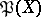 of all subsets of
of all subsets of 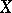 if a one-element set is identified with the element comprising it. When
if a one-element set is identified with the element comprising it. When 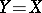 , a set
, a set 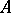 is called an invariant subset for
is called an invariant subset for 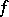 if
if 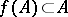 , while a point
, while a point  is called a fixed point for
is called a fixed point for 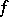 if
if  . Invariant sets and fixed points are important in solving functional equations of the form
. Invariant sets and fixed points are important in solving functional equations of the form 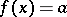 or
or 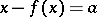 .
.
Every mapping 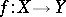 gives rise to a mapping defined on the subsets of the set
gives rise to a mapping defined on the subsets of the set  or
or 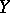 and taking subsets of the set
and taking subsets of the set 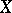 as values. In fact, for every
as values. In fact, for every 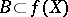 (or
(or 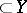 ), the set
), the set 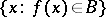 is denoted by
is denoted by 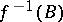 , and is called the complete inverse image (complete pre-image) of
, and is called the complete inverse image (complete pre-image) of 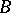 . If
. If 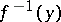 for each
for each 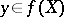 consists of a single element, then
consists of a single element, then 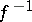 is a mapping of elements, is defined on
is a mapping of elements, is defined on 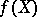 , and takes values in
, and takes values in 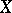 . It is also called the inverse mapping for
. It is also called the inverse mapping for 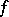 . The existence of an inverse mapping is equivalent to the solvability of the equation
. The existence of an inverse mapping is equivalent to the solvability of the equation  ,
, 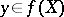 , for a unique
, for a unique  when
when 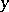 is given.
is given.
If the sets  and
and 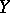 have certain properties, then interesting classes can be distinguished in the set
have certain properties, then interesting classes can be distinguished in the set 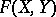 of all mappings from
of all mappings from 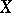 into
into 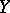 . Thus, for partially ordered sets
. Thus, for partially ordered sets 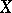 and
and 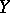 , the mapping
, the mapping 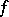 is isotone if
is isotone if 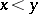 implies
implies  (cf. Isotone mapping). For complex planes
(cf. Isotone mapping). For complex planes 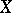 and
and 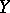 , the class of holomorphic mappings is naturally selected. For topological spaces
, the class of holomorphic mappings is naturally selected. For topological spaces 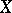 and
and 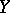 , the class of continuous mappings between these spaces is distinguished naturally; an extended theory of differentiation of mappings (cf. Differentiation of a mapping) has been constructed. For mappings of a scalar argument and, in the most general case, for mappings defined on a measure space, the concept of (weak or strong) measurability can be introduced, and various Lebesgue-type integrals can be constructed (for example, the Bochner integral and the Daniell integral).
, the class of continuous mappings between these spaces is distinguished naturally; an extended theory of differentiation of mappings (cf. Differentiation of a mapping) has been constructed. For mappings of a scalar argument and, in the most general case, for mappings defined on a measure space, the concept of (weak or strong) measurability can be introduced, and various Lebesgue-type integrals can be constructed (for example, the Bochner integral and the Daniell integral).
A mapping is called a multi-valued mapping if subsets 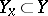 consisting of more than one element are assigned to certain values of
consisting of more than one element are assigned to certain values of  . Examples of this type of mappings include multi-sheeted functions of a complex variable, multi-valued mappings of topological spaces, and others.
. Examples of this type of mappings include multi-sheeted functions of a complex variable, multi-valued mappings of topological spaces, and others.
References
| [1] | N. Bourbaki, "Elements of mathematics. Theory of sets" , Addison-Wesley (1968) (Translated from French) |
| [2] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
| [3] | J.L. Kelley, "General topology" , Springer (1975) |
Comments
For a mapping 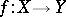 , the set
, the set 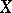 is also called the source of
is also called the source of 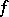 , while
, while 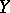 is also called the target of
is also called the target of 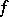 , [a3].
, [a3].
References
| [a1] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
| [a2] | P.R. Halmos, "Naive set theory" , v. Nostrand (1961) |
| [a3] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
Mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mapping&oldid=15615