M-dissipative-operator
From Encyclopedia of Mathematics
Let 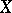 be a real Banach space with dual space
be a real Banach space with dual space 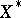 and normalized duality mapping
and normalized duality mapping 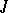 (cf. also Duality; Adjoint space). An operator
(cf. also Duality; Adjoint space). An operator 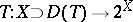 is called dissipative if for every
is called dissipative if for every 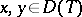 and every
and every 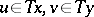 there exists a
there exists a 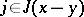 such that
such that 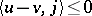 (cf. also Dissipative operator). A dissipative operator
(cf. also Dissipative operator). A dissipative operator 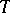 is called
is called 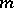 -dissipative if
-dissipative if 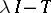 is surjective for all
is surjective for all 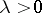 . Thus, an operator
. Thus, an operator 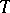 is dissipative (respectively,
is dissipative (respectively, 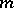 -dissipative) if and only if the operator
-dissipative) if and only if the operator 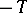 is accretive (respectively,
is accretive (respectively, 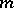 -accretive). For more information, see Accretive mapping and
-accretive). For more information, see Accretive mapping and 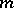 -accretive operator.
-accretive operator.
How to Cite This Entry:
M-dissipative-operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=M-dissipative-operator&oldid=11944
M-dissipative-operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=M-dissipative-operator&oldid=11944
This article was adapted from an original article by A.G. Kartsatos (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article