M-accretive-operator

Let 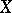be a real Banach space with dual space 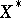and normalized duality mapping 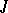(cf. also Duality; Adjoint space). An operator 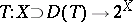is called accretive if for every 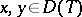and every 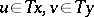there exists a 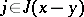such that 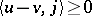(cf. also Accretive mapping). An accretive operator 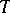is called 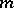-accretive if 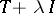is surjective for all 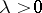(cf. also Surjection). Accretive and 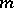-accretive operators were introduced and studied intensively in the late 1960s and early 1970s. V. Barbu, F. Browder, H. Brézis, B.D. Calvert, M.G. Crandall, T. Kato, Y. Komura, A. Pazy, and S. Reich were among the first to recognize the importance and future impact of the class of 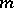-accretive operators.

There are two main problems associated with the class of 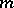-accretive operators: the time-dependent problem and the time-independent problem. The time-dependent problem is usually concerned with the solvability of first- and second-order evolution equations (cf. also Evolution equation), while the time-independent problem deals with equations of elliptic type (cf. also Elliptic partial differential equation). 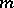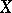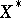Some of the early highlights of the theory, related to the time-dependent problem, include: Kato's fundamental existence result (1967, [a8]), concerning the first-order evolution problem with a time-dependent -accretive operator in a Banach space with uniformly convex (cf. also Banach space); the Crandall–Liggett theorem on generation of semi-groups (1971, [a4]) (in a general Banach space); and the Crandall–Pazy theorem on generation of an evolution operator (1972, [a5]), concerning the first-order evolution problem with a time-dependent 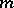-accretive operator in a general Banach space .

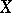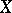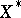Spaces with uniformly convex include all spaces, 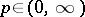. In [a8], T. Kato used the approximate evolution problem involving the Yosida approximants of the single-valued -accretive operator 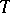: 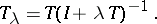In [a4], M.G. Crandall and T. Liggett made use, for the first time, of the classical method of lines in order to show the existence and the representation of the semi-group generated by an 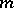-accretive operator 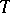in terms of a product formula. The method of lines was used again in [a5] to obtain the product formula of an evolution operator associated with the time-dependent problem. The class of time-dependent problems includes the class of problems involving functional-differential equations of the type

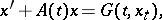(a1)

where 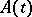is an 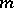-accretive operator. See [a9] for over one hundred references on these and other related problems, as well as for applications to the field of partial differential equations.

The elliptic-type problems often involve sums of time-independent operators, some of which may be accretive or 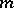-accretive. Several early results for sums of the type 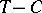, with 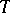accretive and 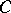compact, may be found in [a2]. In [a2], F. Browder developed degree theories for such operators (with strongly accretive mappings 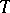), where 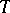is either continuous with 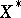uniformly convex, or uniformly continuous in a general Banach space 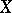. His construction of a degree mapping was based on the Leray–Schauder degree of the mapping 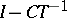on the set 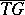(cf. also Degree of a mapping), where 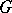is an open set in 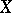. Actually, Browder's degrees can be constructed for more general mappings of the type 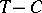, where 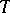is a local homeomorphism. References to many later degree theories, as well a variety of other facts involving accretive and 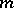-accretive operators, can be found in [a7].

The theory of 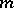-accretive operators parallels the theory of maximal monotone operators in many ways. There are only a few basic properties of maximal monotone operators that do not yet have a counterpart in the class of the 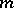-accretive operators.

Naturally, the concept of an 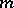-accretive operator extends to complex Banach spaces, where 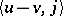above is replaced by .

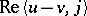References

[a1]	V. Barbu, "Nonlinear semigroups and differential equations in Banach spaces" , Noordhoff (1975)
[a2]	F.E. Browder, "Nonlinear operators and nonlinear equations of evolution in Banach spaces" , Proc. Symp. Pure Math. , 18: 2 , Amer. Math. Soc. (1976)
[a3]	I. Cioranescu, "Geometry of Banach spaces, duality mappings and nonlinear problems" , Kluwer Acad. Publ. (1990)
[a4]	M.G. Crandall, T. Liggett, "Generation of semigroups of nonlinear transformations in general Banach spaces" Amer. J. Math. , 93 (1971) pp. 265–298
[a5]	M.G. Crandall, A. Pazy, "Nonlinear evolution equations in Banach spaces" Israel J. Math. , 11 (1972) pp. 57–94
[a6]	K. Deimling, "Nonlinear functional analysis" , Springer (1985)
[a7]	A.G. Kartsatos, "Recent results involving compact perturbations and compact resolvents of accretive operators in Banach spaces" , Proc. World Congress Nonlinear Analysts, Tampa, Florida (1992) , III , W. de Gruyter (1995) pp. 2197–2222
[a8]	T. Kato, "Nonlinear semigroups and evolution equations" J. Math. Soc. Japan , 19 (1967) pp. 508–520
[a9]	W. Ruess, "Existence of solutions to partial functional differential equations with delay" A.G. Kartsatos (ed.) , Theory and Applications of Nonlinear Operators of Accretive and Monotone Type , M. Dekker (1996) pp. 259–288