Luzin theorem

Luzin's theorem in the theory of functions of a complex variable (the local principle of finite area) is a result of N.N. Luzin that reveals a connection between the boundary properties of an analytic function in the unit disc and the metric of the Riemann surface onto which it maps the disc (see [1], [2]).

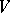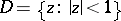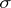Let be any domain inside the unit disc of the complex -plane adjoining an arc of the unit circle 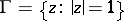, and let

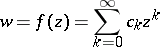be a regular analytic function in 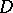. If the area of the Riemann surface that is the image of 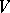under the mapping 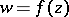is finite, then the series

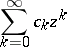converges almost-everywhere on .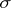

In connection with this theorem Luzin made a conjecture, also known as Luzin's problem. A point 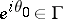is called a Luzin point of the function 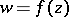if 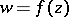maps every disc touching 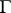from the inside at 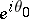onto a domain of infinite area on the Riemann surface of 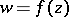. The Luzin conjecture is that there are bounded analytic functions in 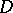such that every point of 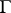is a Luzin point for them. The Luzin conjecture was first confirmed completely in 1955 (see [3]).

References

[1]	N.N. Luzin, "On localization of the finite area principle" Dokl. Akad. Nauk SSSR , 56 (1947) pp. 447–450 (In Russian)
[2]	N.N. Luzin, "Collected works" , 1 , Moscow (1953) pp. 318–330 (In Russian)
[3]	A. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauki i Tekhn. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian)

Comments

The reference for the solution of Luzin's problem is [a1].

References

[a1]	A.J. Lohwater, G. Piranian, "On a conjecture of Luzin" Michigan Math. J. , 3 (1955) pp. 63–68

Luzin's theorems in descriptive set theory are, by convention, split into three parts. The first and main part is directed towards the study of effective sets (analytic, Borel, Luzin (projective) sets). Here one is concerned with the Luzin separability principles and the theorem on the existence of Luzin sets of arbitrary class (cf. Luzin set). The second part is the study of problems lying on the path to the solution of the continuum hypothesis and the problem of the cardinality of -sets (cf. 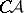-set). Here one distinguishes the Luzin–Sierpiński theorem on partitioning an interval into Borel sets, determined by the corresponding Luzin sieve, and also Luzin's covering theorem: Let 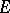and 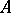be disjoint analytic sets (cf. 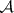-set; Analytic set) and let

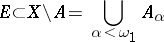be a decomposition of 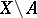into constituents; then there is an index 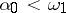such that

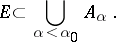The third part contains results obtained by the use of the axiom of choice. Here one borders on philosophical work in set theory. One distinguishes Luzin's theorem on the existence of an uncountable set of the first category (cf. Category of a set) in any perfect set, and on partitioning an interval into an uncountable number of non-measurable sets. To complete this part there is Luzin's theorem on subsets of the set of natural numbers, which reflects some properties of the remainder 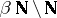of the Stone–Čech compactification 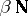of the natural number series .

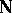References

[1]	N.N. Luzin, "Collected works" , 2 , Moscow (1958) (In Russian)

B.A. Efimov

Comments

See Luzin sieve for the definition of constituents.

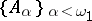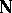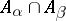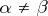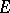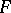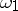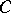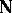"Luzin's theorem on subsets of the set of natural numbers" states that there is a family of infinite subsets of such that is finite for and such that for any two uncountable disjoint subsets and of there is no subset of such that for all 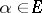: 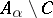is finite and for all 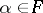: 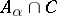is finite. A family like this usually called a Luzin family. See [a2].

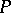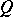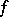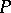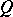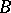In the West, the name "Luzin theorem" refers almost always to a result in measure theory; see Luzin criterion. It may also refer to the following result of Luzin in descriptive set theory: If is a Polish space, a separable metrizable space and is an injective Borel mapping from into , then the direct image of any Borel subset of 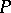is a Borel subset of 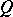. Luzin's covering theorem in descriptive set theory is usually called the (classical) boundness theorem in the West; it gave rise, together with the Luzin–Sierpiński theorem, Luzin sieves, etc., to the modern use of countable ordinals in this theory. See also Descriptive set theory.

References

[a1]	K. Kuratowski, "Topology" , 1 , PWN & Acad. Press (1966) (Translated from French)
[a2]	E.K. van Douwen, "The integers and topology" K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of Set-Theoretic Topology , North-Holland (1984) pp. 111–167
[a3]	R. Engelking, "Hausdorff's gaps and limits and compactifications" , Theory of Sets and Topology (in honour of F. Hausdorff) , Deutsch. Verlag Wissenschaft. (1972) pp. 89–94