Luzin set
projective set
A subset of a complete separable metric space, defined by induction as follows. The Luzin sets of class 0 are the Borel sets (cf. Borel set). The Luzin sets of class 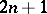 are continuous images of Luzin sets of class
are continuous images of Luzin sets of class 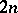 . The Luzin sets of class
. The Luzin sets of class 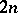 are complements of Luzin sets of class
are complements of Luzin sets of class 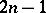 . In particular, Luzin sets of class 1, that is, continuous images of Borel sets, are called analytic sets, or
. In particular, Luzin sets of class 1, that is, continuous images of Borel sets, are called analytic sets, or 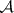 -sets or Suslin sets (cf.
-sets or Suslin sets (cf. 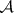 -set; Analytic set). The concept of a Luzin set is due to N.N. Luzin [1]. If the sets
-set; Analytic set). The concept of a Luzin set is due to N.N. Luzin [1]. If the sets 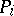 are Luzin sets of class
are Luzin sets of class  , then
, then 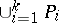 and
and 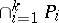 are also Luzin sets of class
are also Luzin sets of class  . If the sets
. If the sets 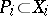 are Luzin sets of class
are Luzin sets of class  lying in complete separable metric spaces
lying in complete separable metric spaces 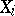 , then the direct product (finite or countable)
, then the direct product (finite or countable) 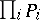 is a Luzin set of class
is a Luzin set of class  in the space
in the space 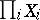 . A Luzin set of odd class
. A Luzin set of odd class  situated in a space
situated in a space 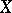 coincides with the projection of a set of class
coincides with the projection of a set of class 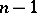 situated in
situated in 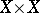 . The space
. The space  of irrational numbers in the interval
of irrational numbers in the interval 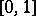 contains, for any
contains, for any 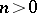 , a Luzin set of class
, a Luzin set of class  that is not a Luzin set of class
that is not a Luzin set of class 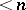 ; the space
; the space  also contains sets that are not Luzin sets.
also contains sets that are not Luzin sets.
References
| [1] | N.N. [N.N. Luzin] Lusin, "Sur un problème de M. Emile Borel et les ensemble projectifs de M. Henri Lebesgue" C.R. Acad. Sci. Paris , 180 (1925) pp. 1318–1320 |
| [2] | N.N. [N.N. Luzin] Lusin, "Leçons sur les ensembles analytiques et leurs applications" , Gauthier-Villars (1930) |
| [3] | K. Kuratowski, "Topology" , 1 , PWN & Acad. Press (1966) (Translated from French) |
Comments
The term "Luzin set" is in the West almost exclusively used for a subset of the real line whose intersection with every nowhere-dense set is countable (see Luzin space). The sets discussed in the main article above are almost exclusively called projective sets (cf. Projective set). The sets of class 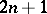 are generally called
are generally called 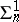 -sets and those of class
-sets and those of class 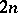 are called
are called 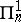 -sets. See Descriptive set theory.
-sets. See Descriptive set theory.
All important problems about projective sets have received satisfactory answers during the last three decades, see Descriptive set theory and Luzin problem.
References
| [a1] | Y.N. Moschovakis, "Descriptive set theory" , North-Holland (1980) |
| [a2] | T.J. Jech, "Set theory" , Acad. Press (1978) pp. 523ff (Translated from German) |
Luzin set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Luzin_set&oldid=18278