Luzin examples
in the theory of functions of a complex variable
Examples that characterize boundary uniqueness properties of analytic functions (see [1], [2]).
1) For any set 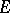 of measure zero on the unit circle
of measure zero on the unit circle  , N.N. Luzin constructed (1919, see [1]) a function
, N.N. Luzin constructed (1919, see [1]) a function 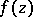 that is regular, analytic and bounded in the unit disc
that is regular, analytic and bounded in the unit disc 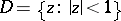 and is such that
and is such that  does not have radial boundary values along each of the radii that end at points of
does not have radial boundary values along each of the radii that end at points of 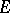 .
.
A similar example of Luzin and I.I. Privalov (1925, see [2], [3]) differs only by insignificant changes.
2) Luzin also constructed (1925, see [2]) regular analytic functions  and
and 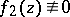 in
in 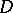 that tend, respectively, to infinity and zero along all radii that end at points of some set of full measure
that tend, respectively, to infinity and zero along all radii that end at points of some set of full measure 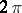 on
on 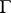 . This set
. This set 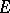 is of the first Baire category (cf. Baire classes) on
is of the first Baire category (cf. Baire classes) on 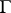 .
.
See also Boundary properties of analytic functions; Luzin–Privalov theorems; Cluster set.
References
| [1] | N.N. Luzin, , Collected works , 1 , Moscow (1953) pp. 267–269 (In Russian) |
| [2] | N.N. Luzin, , Collected works , 1 , Moscow (1953) pp. 280–318 (In Russian) |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [4] | A. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauki i Tekhn. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian) |
Comments
References
| [a1] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9 |
Luzin examples. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Luzin_examples&oldid=18316