Luzin-C-property
A characteristic property of a measurable function that is finite almost-everywhere on its domain of definition. A function 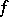 , finite almost-everywhere on
, finite almost-everywhere on 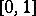 , has the
, has the 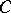 -property on
-property on 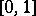 if for every
if for every 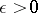 there is a perfect set
there is a perfect set 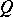 in
in 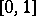 with measure
with measure 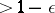 on which
on which 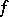 is continuous if considered only on
is continuous if considered only on 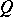 . The
. The 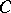 -property was introduced by N.N. Luzin [1], who also proved that for a function to have the
-property was introduced by N.N. Luzin [1], who also proved that for a function to have the  -property it is necessary and sufficient that it be measurable and finite almost-everywhere on
-property it is necessary and sufficient that it be measurable and finite almost-everywhere on 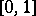 . This theorem of Luzin (the Luzin criterion) can be generalized to the case of functions of several variables (see [3], [4]) and is one of the main theorems in the metric theory of functions.
. This theorem of Luzin (the Luzin criterion) can be generalized to the case of functions of several variables (see [3], [4]) and is one of the main theorems in the metric theory of functions.
References
| [1] | N.N. Luzin, Mat. Sb. , 28 (1912) pp. 266–294 |
| [2] | N.N. Luzin, "Collected works" , 1 , Moscow (1953) (In Russian) |
| [3] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
| [4] | E. Kamke, "Das Lebesgue–Stieltjes Integral" , Teubner (1960) |
Comments
See Luzin criterion for additional references and comments.
Luzin-C-property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Luzin-C-property&oldid=14616