Listing polynomials
Two polynomial invariants of a knot diagram, described by J.B. Listing in 1847 [a1], named by him complexions-symbol (cf. also Knot and link diagrams). Listing associated with every corner of a crossing a symbol  (for dexiotropic, i.e. right-handed) or
(for dexiotropic, i.e. right-handed) or  (for leotropic, i.e. left-handed) according to the convention of Fig.a1a. He then coloured regions cut out by the diagram in a checkerboard manner: black and white and such that neighbouring regions have different colours. To each region he associated a
(for leotropic, i.e. left-handed) according to the convention of Fig.a1a. He then coloured regions cut out by the diagram in a checkerboard manner: black and white and such that neighbouring regions have different colours. To each region he associated a  -variable monomial
-variable monomial 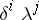 , where
, where  is the number of
is the number of  corners and
corners and  the number of
the number of  corners in the region. The first Listing polynomial, or black Listing polynomial,
corners in the region. The first Listing polynomial, or black Listing polynomial, 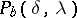 is equal to the sum of the above monomials taken over all black regions. The second Listing polynomial, or white Listing polynomial,
is equal to the sum of the above monomials taken over all black regions. The second Listing polynomial, or white Listing polynomial, 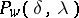 is defined in a similar manner, summing over white regions.
is defined in a similar manner, summing over white regions.
Listing noted that for an alternating knot diagram each region has corners of the same colour, and that his polynomials are in fact one-variable polynomials. He also stated that the left- and right-handed trefoil knots are not equivalent (cf. also Torus knot) and that there are knots without an alternating diagram. He noticed further that his polynomials can change when the knot diagram is modified without changing the knot type.

Figure: l130090a
In his 1849 note, Listing showed that the figure-eight knot, Fig.a1b, and its mirror image are equivalent [a2]. Because of this, this knot is often called the Listing knot.
In modern knot theory, Listing's ideas are widely used: colouring of regions (e.g. to define the Goeritz matrix), labelling of corners (e.g. to define the Kauffman bracket polynomial), studying labelling of corners of alternating diagrams (e.g. to proof the Tait conjectures). Listing polynomials can be thought as a precursors of the partition function of a state model of a physical system in statistical mechanics (cf. also Statistical mechanics, mathematical problems in).
References
| [a1] | J.B. Listing, "Vorstudien zur Topologie" Göttinger Studien (Abt. 1) , 1 (1847) pp. 811–875 |
| [a2] | C.N. Little, "Non-alternate  knots" Trans. Royal Soc. Edinburgh , XXXIX: III : 30 (1899) pp. 771–778 (Read: July 3, 1899) knots" Trans. Royal Soc. Edinburgh , XXXIX: III : 30 (1899) pp. 771–778 (Read: July 3, 1899) |
Listing polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Listing_polynomials&oldid=15378