Lipschitz condition

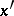A restriction on the behaviour of increase of a function. If for any points and belonging to an interval 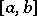the increase of a function 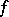satisfies the inequality

(*)

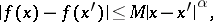where 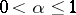and 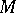is a constant, then one says that 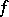satisfies a Lipschitz condition of order 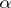on 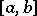and writes 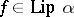, 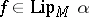or 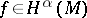. Every function that satisfies a Lipschitz condition with some 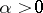on 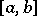is uniformly continuous on 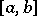, and functions that satisfy a Lipschitz condition of order 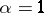are absolutely continuous (cf. Absolute continuity; Uniform continuity). A function that has a bounded derivative on 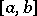satisfies a Lipschitz condition on with any .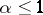

The Lipschitz condition (*) is equivalent to the condition

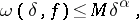where 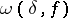is the modulus of continuity (cf. Continuity, modulus of) of 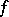on 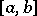. Lipschitz conditions were first considered by R. Lipschitz [1] as a sufficient condition for the convergence of the Fourier series of 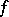. In the case 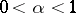the condition (*) is also called a Hölder condition of order .

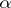References

[1]	R. Lipschitz, "De explicatione per series trigonometricas insttuenda functionum unius variablis arbitrariarum, et praecipue earum, quae per variablis spatium finitum valorum maximorum et minimorum numerum habent infintum disquisitio" J. Reine Angew. Math. , 63 (1864) pp. 296–308
[2]	A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988)
[3]	I.P. Natanson, "Constructive function theory" , 1–3 , F. Ungar (1964–1965) (Translated from Russian)