Lie polynomial

Let 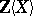denote the free associative algebra over 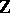in the indeterminates 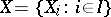. Give bi-algebra and Hopf algebra structures by means of the co-multiplication, antipode, and augmentation defined by:

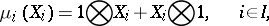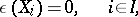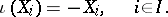Then 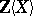becomes the Leibniz–Hopf algebra. A Lie polynomial is an element 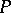of such that 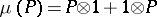, i.e., the Lie polynomials are the primitive elements of the Hopf algebra 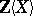(see Primitive element in a co-algebra). These form a Lie algebra 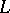under the commutator difference product 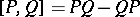. The Lie algebra 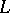is the free Lie algebra on 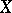over 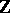(Friedrich's theorem; cf. also Lie algebra, free) and 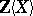is its universal enveloping algebra.

For bases of 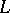viewed as a submodule of 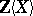, see Hall set; Shirshov basis; Lyndon word. Still other bases, such as the Meier–Wunderli basis and the Spitzer–Foata basis, can be found in [a3].

References

[a1]	N. Bourbaki, "Groupes de Lie" , II: Algèbres de Lie libres , Hermann (1972)
[a2]	C. Reutenauer, "Free Lie algebras" , Oxford Univ. Press (1993)
[a3]	X. Viennot, "Algèbres de Lie libres et monoïdes libres" , Springer (1978)
[a4]	J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965)