Lie group, Banach
A set 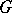 endowed with a group structure and an analytic Banach manifold structure (cf. Banach analytic space) at the same time; these two structures are compatible in the following sense: the mapping
endowed with a group structure and an analytic Banach manifold structure (cf. Banach analytic space) at the same time; these two structures are compatible in the following sense: the mapping  from
from 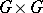 into
into  is analytic. If the Banach manifold is finite dimensional, this concept coincides with the usual concept of a Lie group.
is analytic. If the Banach manifold is finite dimensional, this concept coincides with the usual concept of a Lie group.
Examples. A Banach space with an addition operation, the set  of invertible elements of a Banach algebra
of invertible elements of a Banach algebra  with a multiplication operation, and the set
with a multiplication operation, and the set  of functions smooth of order
of functions smooth of order 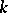 on a smooth manifold
on a smooth manifold  with values in a Lie group
with values in a Lie group 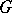 and with the operation of pointwise multiplication, are Banach Lie groups. On the other hand, the set
and with the operation of pointwise multiplication, are Banach Lie groups. On the other hand, the set  of one-to-one mappings smooth of order
of one-to-one mappings smooth of order 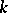 of a smooth manifold
of a smooth manifold 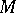 onto itself is not a Banach Lie group: in this case the natural structures of the Banach manifold and the group (with respect to the operation of composition) are not compatible.
onto itself is not a Banach Lie group: in this case the natural structures of the Banach manifold and the group (with respect to the operation of composition) are not compatible.
Some fundamental theorems in the theory of Lie groups remain true for Banach Lie groups: to every Banach Lie group corresponds a Banach Lie algebra, from which in turn one can recover a local Banach Lie group. It is known, however, that not every local Banach Lie group can be extended to a global one [2]; a neighbourhood of the identity of a Banach Lie group is covered by the image of the exponential mapping; there is a correspondence between connected closed subgroups of a Banach Lie group and closed subalgebras of the corresponding Lie algebra.
There are various generalizations of the concept of a Banach Lie group (see [3]), in which the Banach space structure is replaced by a linear topological space structure of more general type.
References
| [1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [2] | P. de la Harpe, "Classical Banach–Lie algebras and Banach–Lie groups of operators in Hilbert space" , Springer (1972) |
| [3] | H. Omori, "Infinite dimensional Lie transformation groups" , Springer (1974) |
Lie group, Banach. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_group,_Banach&oldid=11260