Lie algebra, supersolvable
triangular Lie algebra
A finite-dimensional Lie algebra  over a field
over a field  for which the eigen values of the operators
for which the eigen values of the operators  of the adjoint representation belong to
of the adjoint representation belong to  for all
for all  (cf. Adjoint representation of a Lie group).
(cf. Adjoint representation of a Lie group).
A supersolvable Lie algebra is solvable. The class of supersolvable Lie algebras contains the class of nilpotent Lie algebras and is contained in the class of exponential Lie algebras (cf. Lie algebra, nilpotent; Lie algebra, exponential). It is closed with respect to transition to subalgebras, quotient algebras and finite direct sums, but it is not closed with respect to extensions.
A supersolvable Lie algebra over a perfect field has many of the properties of solvable Lie algebras (cf. Lie algebra, solvable) over an algebraically closed field (Lie's theorem, the presence of a chain of ideals  for which
for which  , and others). In an arbitrary finite-dimensional Lie algebra
, and others). In an arbitrary finite-dimensional Lie algebra  there are maximal supersolvable subalgebras and they contain the nil radical. If
there are maximal supersolvable subalgebras and they contain the nil radical. If  or
or  , or if
, or if 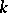 is perfect and
is perfect and  is an algebraic linear Lie algebra, then all supersolvable subalgebras are conjugate. The Lie algebra
is an algebraic linear Lie algebra, then all supersolvable subalgebras are conjugate. The Lie algebra  over
over  corresponding to a
corresponding to a  -split algebraic group (cf. Split group) over a perfect field
-split algebraic group (cf. Split group) over a perfect field 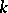 is a supersolvable Lie algebra.
is a supersolvable Lie algebra.
Any supersolvable Lie algebra over a field of characteristic 0 can be isomorphically imbedded in the Lie algebra of upper-triangular matrices with coefficients from 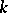 (which is itself supersolvable). The simplest example of a supersolvable Lie algebra that is not nilpotent is a two-dimensional Lie algebra with basis
(which is itself supersolvable). The simplest example of a supersolvable Lie algebra that is not nilpotent is a two-dimensional Lie algebra with basis 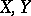 and defining relation
and defining relation  . For references see Lie group, supersolvable.
. For references see Lie group, supersolvable.
Lie algebra, supersolvable. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_algebra,_supersolvable&oldid=17913