Lie algebra, solvable

A Lie algebra 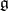over a field 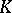satisfying one of the following equivalent conditions:

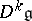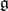1) the terms of the derived series of are equal to 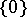for sufficiently large ;

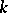2) there is a finite decreasing chain of ideals 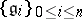of 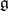such that 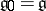, 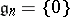and 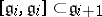(that is, the Lie algebras 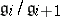are Abelian for all );

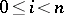3) there is a finite decreasing chain of subalgebras 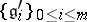such that 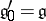, , 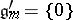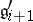is an ideal of 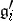, and 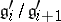is a one-dimensional (Abelian) Lie algebra for .

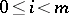A nilpotent Lie algebra (cf. Lie algebra, nilpotent) is solvable. If 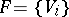is a complete flag in a finite-dimensional vector space 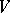over 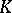, then

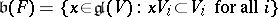is a solvable subalgebra of the Lie algebra 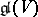of all linear transformations of 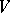. If one chooses a basis in 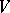compatible with , then with respect to that basis, elements of 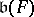are represented by upper triangular matrices; the resulting solvable linear Lie algebra is denoted by 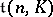, where .

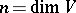The class of solvable Lie algebras is closed with respect to transition to a subalgebra, a quotient algebra or an extension. In particular, any subalgebra of 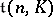is solvable. If 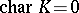and 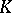is an algebraically closed field, then any finite-dimensional solvable Lie algebra is isomorphic to a subalgebra of 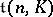for some . One of the main properties of solvable Lie algebras is expressed in Lie's theorem: Let 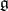be a solvable Lie algebra over an algebraically closed field of characteristic and let 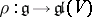be a finite-dimensional linear representation of it. Then in 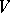there is a complete flag 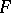such that 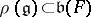. In particular, if 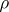is irreducible, then 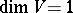. Ideals of 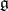can be chosen so as to form a complete flag, that is, so that .

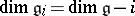A finite-dimensional Lie algebra 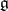over a field of characteristic is solvable if and only if the algebra is nilpotent. Another criterion for solvability (Cartan's criterion) is: 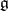is solvable if and only if 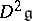is orthogonal to the whole of 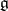with respect to the Killing form (or any bilinear form associated with a faithful finite-dimensional representation of ).

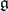Solvable Lie algebras were first considered by S. Lie in connection with the study of solvable Lie transformation groups. The study of solvable Lie algebras acquired great significance after the introduction of the concept of the radical (that is, the largest solvable ideal) of an arbitrary finite-dimensional Lie algebra 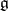, and it was proved that in the case 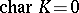the algebra 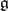is the semi-direct sum of its radical and a maximal semi-simple subalgebra (see Levi–Mal'tsev decomposition). This made it possible to reduce the problem of classifying arbitrary Lie algebras to the enumeration of semi-simple (which for 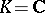had already been done by W. Killing) and solvable Lie algebras. The classification of solvable Lie algebras (f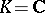or or 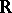) has been carried out only in dimensions .

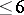If 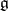is a solvable algebraic subalgebra (cf. Algebraic algebra) of 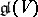, where 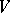is a finite-dimensional space over a field 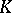of characteristic , then 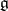splits into the semi-direct product of the nilpotent ideal formed by all nilpotent transformations of 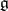and the Abelian subalgebra consisting of the semi-simple transformations [6]. In general, any split solvable Lie algebra, that is, a finite-dimensional solvable Lie algebra over 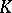every element of which splits into a sum 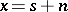, where 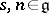, , 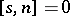is semi-simple, and is nilpotent, has a similar structure [8]. To every finite-dimensional solvable Lie algebra over 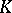there uniquely corresponds a minimal split solvable Lie algebra containing it (the Mal'tsev decomposition). The problem of classifying solvable Lie algebras that have a given Mal'tsev decomposition has been solved [8]. Thus, the problem of classifying solvable Lie algebras reduces, in a certain sense, to the study of nilpotent Lie algebras.

Apart from the radical, in an arbitrary finite-dimensional Lie algebra 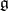one can distinguish maximal solvable subalgebras. If 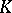is an algebraically closed field of characteristic , then all such subalgebras of 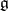(they are called Borel subalgebras) are conjugate. For example, is a Borel subalgebra of the Lie algebra of all matrices of order . If 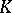is not algebraically closed or if 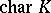is finite, then Lie's theorem is false, in general. However, it can be extended to the case when is perfect and contains the characteristic roots of all the characteristic polynomials 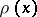of the adjoint transformations 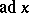, 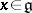. If this condition is satisfied for the adjoint representation of a solvable Lie algebra 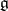(cf. Adjoint representation of a Lie group), then 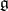is said to be triangular. Many properties of solvable Lie algebras over an algebraically closed field carry over to triangular Lie algebras. In particular, if 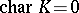, then all maximal triangular subalgebras of an arbitrary finite-dimensional Lie algebra are conjugate (see [1], [7]). Maximal triangular subalgebras are used in the study of semi-simple Lie algebras over an algebraically non-closed field as a good analogue of Borel subalgebras. They also play a fundamental role in the description of the connected uniform subgroups (cf. Uniform subgroup) of Lie groups [9].

References

[1]	A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150
[2]	N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)
[3]	N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979))
[4]	A. Borel, "Linear algebraic groups" , Benjamin (1969)
[5]	J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French)
[6]	C. Chevalley, "Théorie des groupes de Lie" , 3 , Hermann (1955)
[7]	E.B. Vinberg, "The Morozov–Borel theorem for real Lie groups" Soviet Math. Dokl. , 2 (1961) pp. 1416–1419 Dokl. Akad. Nauk SSSR , 141 (1961) pp. 270–273
[8]	A.I. Mal'tsev, "Solvable Lie algebras" Izv. Akad. Nauk SSSR , 9 (1945) pp. 329–352 (In Russian)
[9]	A.L. Onishchik, "On Lie groups transitive on compact manifolds II" Math. USSR Sb. , 3 (1967) pp. 373–388 Mat. Sb. , 74 (1967) pp. 398–416

References

[a1]	J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972)