Lie algebra, nil
A Lie algebra 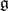 over a field
over a field 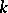 defined by the presence of a function
defined by the presence of a function  such that
such that  , where
, where  , for any
, for any  . The main question about nil Lie algebras concerns the conditions on
. The main question about nil Lie algebras concerns the conditions on  ,
,  ,
,  under which
under which  is (locally) nilpotent (see Lie algebra, nilpotent). A nil Lie algebra that is finite-dimensional over
is (locally) nilpotent (see Lie algebra, nilpotent). A nil Lie algebra that is finite-dimensional over  is nilpotent. On the other hand, over any field there are finitely-generated nil Lie algebras that are not nilpotent [1]. Suppose that
is nilpotent. On the other hand, over any field there are finitely-generated nil Lie algebras that are not nilpotent [1]. Suppose that  is a constant. A nil Lie algebra is locally nilpotent if
is a constant. A nil Lie algebra is locally nilpotent if 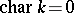 or if
or if  , where
, where  (Kostrikin's theorem, [2]). Local nilpotency also holds in the case when
(Kostrikin's theorem, [2]). Local nilpotency also holds in the case when  is locally solvable. An infinitely-generated nil Lie algebra is not necessarily nilpotent if
is locally solvable. An infinitely-generated nil Lie algebra is not necessarily nilpotent if 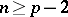 (see [3]), and for
(see [3]), and for 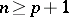 non-nilpotency can still occur under the condition of solvability. Recently it has been proved by E.I. Zel'myanov that a nil Lie algebra is nilpotent if
non-nilpotency can still occur under the condition of solvability. Recently it has been proved by E.I. Zel'myanov that a nil Lie algebra is nilpotent if  (cf. [6]) and that a nil algebra is also locally nilpotent if
(cf. [6]) and that a nil algebra is also locally nilpotent if 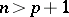 . The study of nil Lie algebras over a field
. The study of nil Lie algebras over a field  of characteristic
of characteristic  is closely connected with the Burnside problem.
is closely connected with the Burnside problem.
References
| [1] | E.S. Golod, "On nil-algebras and residually finite groups" Izv. Akad. Nauk SSSR Ser. Mat. , 28 : 2 (1964) pp. 273–276 (In Russian) |
| [2] | A.I. Kostrikin, "On Burnside's problem" Izv. Akad. Nauk SSSR Ser. Mat. , 23 : 1 (1959) pp. 3–34 (In Russian) |
| [3] | Yu.P. Razmyslov, "On Lie algebras satisfying the Engel condition" Algebra and Logic , 10 : 1 (1971) pp. 21–29 Algebra i Logika , 10 : 1 (1971) pp. 33–44 |
| [4] | Yu. [Yu.A. Bakhturin] Bahturin, "Lectures on Lie algebras" , Akademie Verlag (1978) |
| [5] | A. Braun, "Lie rings and the Engel condition" J. of Algebra , 31 (1974) pp. 287–292 |
| [6] | A.I. Kostrikin, "Around Burnside" , Springer (1989) (Translated from Russian) |
Comments
References
| [a1] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [a2] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 |
Lie algebra, nil. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_algebra,_nil&oldid=13081