Lee-Friedrichs model
What is known today (1998) as the Lee–Friedrichs model [a1], [a2] is characterized by a self-adjoint operator 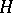 on a Hilbert space
on a Hilbert space 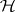 , which is the sum of two self-adjoint operators
, which is the sum of two self-adjoint operators 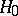 and
and 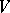 such that
such that 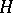 ,
, 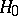 and
and 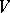 have a common domain,
have a common domain,  has absolutely continuous spectrum (of uniform multiplicity) except for the end-point of the semi-bounded from below spectrum, and one or more eigenvalues which may or may not be embedded in the continuum (cf. also Spectrum of an operator; Absolute continuity). The operator
has absolutely continuous spectrum (of uniform multiplicity) except for the end-point of the semi-bounded from below spectrum, and one or more eigenvalues which may or may not be embedded in the continuum (cf. also Spectrum of an operator; Absolute continuity). The operator 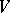 is compact and of finite rank (cf. also Compact operator; Rank), and induces a mapping from the subspace of
is compact and of finite rank (cf. also Compact operator; Rank), and induces a mapping from the subspace of 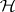 spanned by the eigenvectors of
spanned by the eigenvectors of 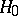 to the subspace corresponding to the continuous spectrum (and the reverse). The central idea of the model is that
to the subspace corresponding to the continuous spectrum (and the reverse). The central idea of the model is that 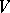 does not map the subspace corresponding to the continuous spectrum into itself, and, as a consequence, the model becomes solvable in the sense described below.
does not map the subspace corresponding to the continuous spectrum into itself, and, as a consequence, the model becomes solvable in the sense described below.
In the physical applications of the model, 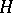 corresponds to the Hamiltonian operator, the self-adjoint operator (often the self-adjoint completion of an essentially self-adjoint operator) that generates the unitary evolution (through the Schrödinger equation) of the vector in
corresponds to the Hamiltonian operator, the self-adjoint operator (often the self-adjoint completion of an essentially self-adjoint operator) that generates the unitary evolution (through the Schrödinger equation) of the vector in 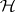 representing the state of the physical system in time (cf. also Hamilton operator).
representing the state of the physical system in time (cf. also Hamilton operator).
The resolvent 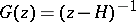 generated by the Laplace transform on
generated by the Laplace transform on 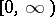 by
by 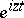 on the Schrödinger evolution operator
on the Schrödinger evolution operator 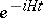 (both acting on some suitable
(both acting on some suitable 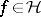 ) is analytic in the upper half
) is analytic in the upper half  -plane. Denoting by
-plane. Denoting by  (with Lebesgue measure
(with Lebesgue measure 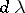 ) the representation of
) the representation of 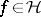 on the continuous spectrum
on the continuous spectrum 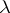 of
of 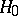 on
on 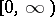 and by
and by  the eigenvector with eigenvalue
the eigenvector with eigenvalue 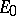 (assuming for the sake of argument just one discrete eigenvector), one sees that the second resolvent equation
(assuming for the sake of argument just one discrete eigenvector), one sees that the second resolvent equation
 | (a1) |
where 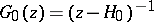 , can be exactly solved by the pair of equations
, can be exactly solved by the pair of equations
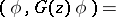 | (a2) |
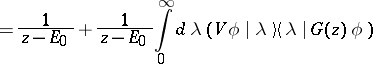 |
and
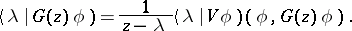 | (a3) |
Substituting (a3) into (a2), one sees that
 | (a4) |
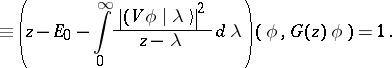 |
If the discrete spectral value 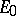 is separated from the continuum (
is separated from the continuum (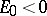 ), then
), then 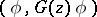 has a pole on the real axis at the point
has a pole on the real axis at the point
 | (a5) |
If 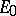 is embedded in the continuum that lies on
is embedded in the continuum that lies on 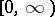 (
( ), one can avoid the generation of a real pole on the negative half-line by the inequality
), one can avoid the generation of a real pole on the negative half-line by the inequality
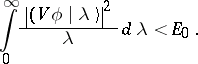 |
The projection of the time evolution of the quantum-mechanical state represented by 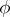 back onto the initial state is given by (using units in which
back onto the initial state is given by (using units in which 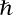 , the Planck constant divided by
, the Planck constant divided by  , is unity):
, is unity):
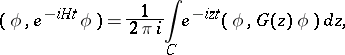 | (a6) |
where the contour goes from 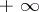 in the negative direction of the real axis and a small distance above it, around the branch point counter-clockwise at
in the negative direction of the real axis and a small distance above it, around the branch point counter-clockwise at  , and back to
, and back to  below the real axis. The construction defined on the left-hand side of (a6) was used by E.P. Wigner and V.F. Weisskopf [a3], [a28] in 1930 as a model for the description of unstable systems; they used it to calculate the line-width of a radiating atom.
below the real axis. The construction defined on the left-hand side of (a6) was used by E.P. Wigner and V.F. Weisskopf [a3], [a28] in 1930 as a model for the description of unstable systems; they used it to calculate the line-width of a radiating atom.
The contour of the integral in (a6) can be deformed so that the integration below the real line is shifted to the negative imaginary axis where, for 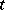 sufficiently positive, this contribution can be considered as negligible (except near the branch cut). The integral path above the real axis can be similarly deformed into the second Riemann sheet of the function
sufficiently positive, this contribution can be considered as negligible (except near the branch cut). The integral path above the real axis can be similarly deformed into the second Riemann sheet of the function  to the negative real axis, but there is a possibility that the second sheet extension of this function has a pole in the lower half-plane. One observes this in the Lee–Friedrichs model [a1], [a2] by studying (for
to the negative real axis, but there is a possibility that the second sheet extension of this function has a pole in the lower half-plane. One observes this in the Lee–Friedrichs model [a1], [a2] by studying (for 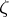 real)
real)
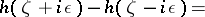 |
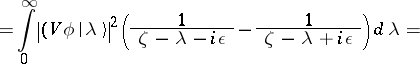 |
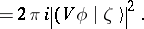 |
Choosing a 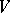 so that
so that 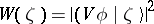 is the boundary value on the real axis of an analytic function in some (sufficiently large) domain in the lower half-plane, one sees that the second sheet continuation of
is the boundary value on the real axis of an analytic function in some (sufficiently large) domain in the lower half-plane, one sees that the second sheet continuation of 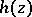 is
is
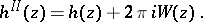 | (a7) |
Now,
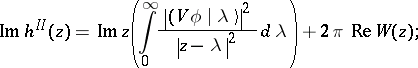 |
if the value of  looked for is sufficiently close to the real axis,
looked for is sufficiently close to the real axis, 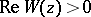 , and
, and 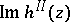 may have a zero for
may have a zero for 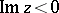 . If the real part vanishes as well, one has a pole of
. If the real part vanishes as well, one has a pole of 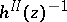 at, say
at, say 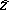 , which implies a decay law of the time evolution of the so-called survival amplitude (a6), of the form
, which implies a decay law of the time evolution of the so-called survival amplitude (a6), of the form 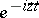 , an exponential decay. The imaginary part of
, an exponential decay. The imaginary part of 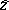 is the semi-decay width computed in lowest-order perturbation theory by Wigner and Weisskopf [a3], [a28].
is the semi-decay width computed in lowest-order perturbation theory by Wigner and Weisskopf [a3], [a28].
In quantum-mechanical scattering theory [a4], [a11], the scattered wave is expressed in terms of an operator-valued function of  ,
,
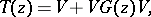 | (a8) |
analytic in the same domain as  . The transition amplitude
. The transition amplitude 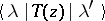 contains, by the hypotheses of the Lee–Friedrichs model, the reduced resolvent
contains, by the hypotheses of the Lee–Friedrichs model, the reduced resolvent 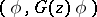 , and the second sheet pole discussed above dominates the behaviour of the scattering for an interval of energies near the real part of
, and the second sheet pole discussed above dominates the behaviour of the scattering for an interval of energies near the real part of 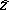 , appearing as a scattering resonance. Hence the Lee–Friedrichs model offers an opportunity to describe scattering and resonance phenomena, along with the behaviour of an unstable system, in the framework of a single mathematical model [a5].
, appearing as a scattering resonance. Hence the Lee–Friedrichs model offers an opportunity to describe scattering and resonance phenomena, along with the behaviour of an unstable system, in the framework of a single mathematical model [a5].
The pole in 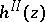 at
at 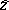 suggests that, in some sense, there may be an eigenvalue equation of the form
suggests that, in some sense, there may be an eigenvalue equation of the form
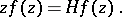 | (a9) |
This equation is exactly solvable in the Lee–Friedrichs model, with
 | (a10) |
but the eigenvalue equation (a9) is satisfied only after analytic continuation to 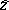 in the same way as described above. This analytic continuation can be done in terms of the sesquilinear form
in the same way as described above. This analytic continuation can be done in terms of the sesquilinear form 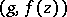 for a suitable
for a suitable 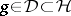 , such that
, such that 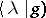 is the boundary value of an analytic function on an adequate domain in the lower half-plane (including the point
is the boundary value of an analytic function on an adequate domain in the lower half-plane (including the point 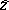 within its boundary). (The eigenfunction
within its boundary). (The eigenfunction 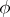 must lie in
must lie in 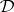 as well.) The Banach space functional
as well.) The Banach space functional 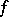 defined in this way lies in the space
defined in this way lies in the space 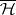 dual to
dual to 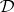 , for which
, for which 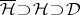 , i.e., an element of a Gel'fand triple (cf. Rigged Hilbert space) [a6], [a7], [a12], [a13], [a14], [a15], [a16], [a17]. This construction has provided the basis for useful physical applications [a8], [a27], [a18], [a19], [a20], [a21], [a22].
, i.e., an element of a Gel'fand triple (cf. Rigged Hilbert space) [a6], [a7], [a12], [a13], [a14], [a15], [a16], [a17]. This construction has provided the basis for useful physical applications [a8], [a27], [a18], [a19], [a20], [a21], [a22].
Note that the quantity 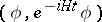 studied in the Wigner–Weisskopf theory [a3], [a28] can never be precisely exponential in form (i.e., more generally,
studied in the Wigner–Weisskopf theory [a3], [a28] can never be precisely exponential in form (i.e., more generally, 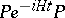 , where
, where 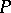 is a projection, cannot be a semi-group) [a9], [a23] although for sufficiently large (but not too large)
is a projection, cannot be a semi-group) [a9], [a23] although for sufficiently large (but not too large) 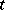 , it may well approximate an exponential. For example, the
, it may well approximate an exponential. For example, the 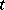 -derivative of
-derivative of 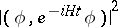 at
at 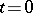 vanishes if
vanishes if 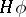 is defined. The time dependence of the Gel'fand triple function may, however, be exactly exponential (if
is defined. The time dependence of the Gel'fand triple function may, however, be exactly exponential (if 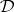 is sufficiently stable).
is sufficiently stable).
Lee's original model [a1], formulated in the framework of non-relativistic quantum field theory, was motivated by an interest in the process of renormalization; it can be seen from (a5) that the interaction 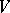 induces a shift in the point spectrum. There is a conserved quantum number in Lee's field theory which enables the model to be written in one sector as a quantum-mechanical model equivalent to the structure used by K.O. Friedrichs [a2], whose motivation was to study the general framework of the perturbation of continuous spectra.
induces a shift in the point spectrum. There is a conserved quantum number in Lee's field theory which enables the model to be written in one sector as a quantum-mechanical model equivalent to the structure used by K.O. Friedrichs [a2], whose motivation was to study the general framework of the perturbation of continuous spectra.
A relativistically covariant form of the Lee–Friedrichs model has been developed in [a10] (see also [a24], [a25], [a26]).
References
| [a1] | T.D. Lee, "Some special exampls in renormalizable field theory" Phys. Rev , 95 (1954) pp. 1329–1334 |
| [a2] | K.O. Friedrichs, "On the perturbation of continuous spectra" Commun. Pure Appl. Math. , 1 (1948) pp. 361–406 |
| [a3] | V.F. Weisskopf, E.P. Wigner, "Berechnung der natürlichen Linienbreite auf Grund der Diracschen Lichttheorie" Z. Phys. , 63 (1930) pp. 54 |
| [a4] | J.R. Taylor, "Scattering theory" , Wiley (1972) |
| [a5] | L.P. Horwitz, J.-P. Marchand, "The decay scattering system" Rocky Mtn. J. Math. , 1 (1971) pp. 225–253 |
| [a6] | I.M. Gel'fand, G.E. Shilov, "Generalized functions" , 4 , Acad. Press (1968) |
| [a7] | W. Baumgartel, "Resonances of perturbed self-adjoint operators and eigenfunctions" Math. Nachr. , 75 (1976) pp. 133–151 |
| [a8] | D. Cocolicchio, Phys. Rev , 57 (1998) pp. 7251 |
| [a9] | L.P. Horwitz, J.-P. Marchand, J. LaVita, "The inverse decay problem" J. Math. Phys. , 12 (1971) pp. 2537–2543 |
| [a10] | L.P. Horwitz, Found. Phys. , 25 (1995) pp. 39 |
| [a11] | R.J. Newton, "Scattering theory of particles and waves" , McGraw-Hill (1976) |
| [a12] | T. Bailey, W.C. Schieve, "Complex energy eigenstates in quantum decay models" Nuovo Cim. , 47A (1978) pp. 231–250 |
| [a13] | A. Bohm, "The rigged Hilbert space and quantum mechanics" , Lecture Notes Physics , 78 , Springer (1978) |
| [a14] | L.P. Horwitz, I.M. Sigal, "On a mathematical model for non-stationary physical systems" Helv. Phys. Acta , 51 (1980) pp. 685–715 |
| [a15] | G. Parravicini, V. Gorini, E.C.G. Sudarshan, "Resonances, scattring theory, and rigged Hilbert spaces" J. Math. Phys. , 21 (1980) pp. 2208–2226 |
| [a16] | A. Bohm, M. Gadella, G.B. Mainland, "Gamow vectors and decaying states" Amer. J. Phys. , 57 (1989) pp. 1103–1108 |
| [a17] | A. Bohm, M. Gadella, "Dirac kets, Gamow vectors and Gel'fand triples" , Lecture Notes Physics , 348 , Springer (1989) |
| [a18] | A. Grecos, I. Prigogine, Proc. Nat. Acad. Sci. USA , 60 (1972) pp. 1629 |
| [a19] | T. Petroski, I. Prigogine, S. Tasaki, Physica A , 175 (1991) pp. 175 |
| [a20] | I. Antoniou, I. Prigogine, Physica A , 192 (1993) pp. 443 |
| [a21] | I. Antoniou, S. Tasaki, Internat. J. Quant. Chem. , 44 (1993) pp. 425 |
| [a22] | I. Antoniou, L. Dmitrieva, Y. Kuperin, Y. Melnikov, "Resonances and the extension of dynamics to rigged Hilbert spaces" Comput. Math. Appl. , 34 (1997) pp. 399–425 |
| [a23] | D.N. Williams, "Difficulty with a kinematic concept of unstable particles: the Sz.-Nagy extension and the Matthews–Salam–Zwanziger representation" Comm. Math. Phys. , 21 (1971) pp. 314–333 |
| [a24] | C.J. Hammer, T.A. Weber, "Field theory for stable and unstable particles" Phys. Rev. , D5 (1972) pp. 3087–3102 |
| [a25] | D.N. Williams, "Large width in the Lee model for the Higgs–Goldstone sector" Nucl. Phys. , B264 (1986) pp. 423–436 |
| [a26] | I. Antoniou, M. Gadella, I. Prigogine, G.P. Pronko, "Relativistic Gamow vectors" J. Math. Phys. , 39 (1998) pp. 2995–3018 |
| [a27] | A. Grecos, I. Prigogine, "Kinetic and ergodic properties of quantum systems: the Friedrichs model" Physica , 59 (1972) pp. 77–96 |
| [a28] | V.F. Weisskopf, E.P. Wigner, "Ueber die natürliche Linienbreite in der Strahlung des harmonischen Oszillators" Z. Phys. , 65 (1930) pp. 18 |
Lee-Friedrichs model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lee-Friedrichs_model&oldid=11926