Law of inertia
for quadratic forms
The theorem stating that for any way of reducing a quadratic form (cf. also Quadratic forms, reduction of)
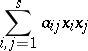 |
with real coefficients to a sum of squares
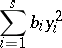 |
by a linear change of variables
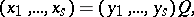 |
where  is a non-singular matrix with real coefficients, the number
is a non-singular matrix with real coefficients, the number  (respectively,
(respectively,  ) of indices
) of indices  for which
for which  (or
(or  ) is fixed. In its classical form, the law of inertia was established by J.J. Sylvester. This statement is sometimes called Sylvester's theorem.
) is fixed. In its classical form, the law of inertia was established by J.J. Sylvester. This statement is sometimes called Sylvester's theorem.
In its modern form, the law of inertia is the following statement concerning properties of symmetric bilinear forms over ordered fields. Let 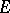 be a finite-dimensional vector space over an ordered field
be a finite-dimensional vector space over an ordered field  , endowed with a non-degenerate symmetric bilinear form
, endowed with a non-degenerate symmetric bilinear form 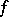 . Then there exists an integer
. Then there exists an integer 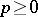 such that for any orthogonal basis
such that for any orthogonal basis  in
in 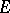 with respect to
with respect to 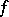 there exist among the
there exist among the  elements
elements
 |
exactly 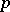 positive and exactly
positive and exactly 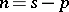 negative ones. The pair
negative ones. The pair 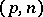 is called the signature of
is called the signature of 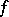 , and the number
, and the number  its index of inertia. Two equivalent forms have the same signature. If
its index of inertia. Two equivalent forms have the same signature. If  is a Euclidean field, equality of signatures is a sufficient condition for the equivalence of bilinear forms. If the index of inertia
is a Euclidean field, equality of signatures is a sufficient condition for the equivalence of bilinear forms. If the index of inertia 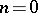 , the form is called positive definite, and for
, the form is called positive definite, and for 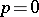 , negative definite. These cases are characterized by the property that
, negative definite. These cases are characterized by the property that 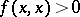 (respectively,
(respectively, 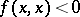 ) for any non-zero
) for any non-zero  . It follows from the law of inertia that
. It follows from the law of inertia that 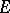 is an orthogonal direct sum (with respect to
is an orthogonal direct sum (with respect to 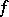 ) of subspaces,
) of subspaces,
 |
such that the restriction of 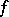 to
to 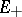 is positive definite while the restriction of
is positive definite while the restriction of 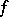 to
to  is negative definite and
is negative definite and
 |
(so that the dimensions of 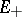 and
and 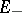 do not depend on the decomposition).
do not depend on the decomposition).
Sometimes the signature of  is taken to be the difference
is taken to be the difference
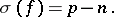 |
If two forms  and
and 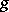 determine the same element of the Witt ring
determine the same element of the Witt ring 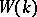 of the field
of the field 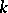 , then
, then 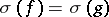 . Furthermore,
. Furthermore, 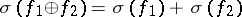 and
and 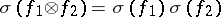 for any non-degenerate forms
for any non-degenerate forms 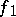 and
and 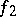 , and
, and 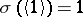 , so that the mapping
, so that the mapping  defines a homomorphism from
defines a homomorphism from 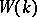 into the ring of integers
into the ring of integers  . If
. If 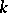 is a Euclidean field, then this homomorphism is an isomorphism.
is a Euclidean field, then this homomorphism is an isomorphism.
The law of inertia can be generalized to the case of a Hermitian bilinear form over a maximal ordered field 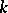 , over a quadratic extension of
, over a quadratic extension of  or over the skew-field of quaternions over
or over the skew-field of quaternions over 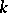 (see [1], [4]).
(see [1], [4]).
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [3] | E. Artin, "Geometric algebra" , Interscience (1957) |
| [4] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) |
Comments
The name index is also used for 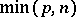 .
.
Law of inertia. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Law_of_inertia&oldid=12928