L-function
A generalization of the zeta-function at the cost of introducing characters (cf. Character of a group). The  -functions form a complicated class of special functions of a complex variable, defined by a Dirichlet series or an Euler product with characters. They are the basic instrument for studying by analytic methods the arithmetic of corresponding mathematical objects: the field of rational numbers, algebraic fields, algebraic varieties over finite fields, etc. The simplest representatives of
-functions form a complicated class of special functions of a complex variable, defined by a Dirichlet series or an Euler product with characters. They are the basic instrument for studying by analytic methods the arithmetic of corresponding mathematical objects: the field of rational numbers, algebraic fields, algebraic varieties over finite fields, etc. The simplest representatives of  -functions are the Dirichlet
-functions are the Dirichlet  -functions (cf. Dirichlet
-functions (cf. Dirichlet  -function). The remaining
-function). The remaining  -functions are more or less close analogues and generalizations of these
-functions are more or less close analogues and generalizations of these  -functions.
-functions.
Comments
Nowadays  -functions comprise a very large class of functions which are attached to representations of the Galois group
-functions comprise a very large class of functions which are attached to representations of the Galois group  . For example, choose a representation
. For example, choose a representation  of the Galois group
of the Galois group 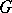 of an algebraic number field
of an algebraic number field 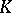 (cf. Representation of a group). For each prime
(cf. Representation of a group). For each prime 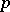 , let
, let 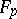 be a Frobenius element in
be a Frobenius element in  . Then the function
. Then the function
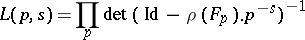 |
is the Artin  -series corresponding to
-series corresponding to 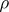 . In a similar way, the action of
. In a similar way, the action of  on the
on the  -torsion points of an elliptic curve
-torsion points of an elliptic curve 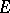 , defined over
, defined over  , gives rise to the Hasse–Weil
, gives rise to the Hasse–Weil  -function of
-function of  . There exists a large body of fascinating conjectures about these
. There exists a large body of fascinating conjectures about these  -functions, which, on the one hand, relate them to automorphic forms (Langlands' conjectures) and, on the other hand, relate values at integral points to algebraic-geometric invariants (Beilinson's conjectures).
-functions, which, on the one hand, relate them to automorphic forms (Langlands' conjectures) and, on the other hand, relate values at integral points to algebraic-geometric invariants (Beilinson's conjectures).
References
| [a1] | S. Gelbart, "An elementary introduction to the Langlands program" Bull. Amer. Math. Soc. , 10 (1984) pp. 177–220 |
| [a2] | M. Rapoport (ed.) N. Schappacher (ed.) P. Schneider (ed.) , Beilinson's conjectures on special values of 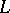 -functions , Acad. Press (1988) -functions , Acad. Press (1988) |
L-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L-function&oldid=19281