Kummer extension
An extension of a field 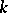 of characteristic
of characteristic 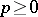 , of the type
, of the type
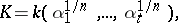 | (1) |
where 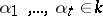 ,
,  is some natural number, and it is assumed that
is some natural number, and it is assumed that 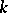 contains a primitive
contains a primitive  -th root of unity
-th root of unity 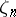 (in particular,
(in particular,  is prime to
is prime to 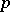 if
if 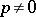 ). Kummer extensions are named after E. Kummer, who first studied extensions of the type
). Kummer extensions are named after E. Kummer, who first studied extensions of the type 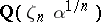 , where
, where 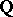 is the field of rational numbers and
is the field of rational numbers and 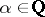 .
.
The main result of the theory of Kummer extensions is that if the field 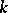 contains a primitive root
contains a primitive root 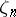 , then a finite extension
, then a finite extension 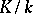 is Kummer (for a given
is Kummer (for a given  ) if and only if
) if and only if 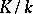 is a normal Abelian extension and the Galois group
is a normal Abelian extension and the Galois group 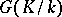 is annihilated by
is annihilated by  . Any Kummer extension of a field
. Any Kummer extension of a field 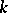 is completely determined by its Kummer group
is completely determined by its Kummer group 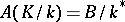 , where
, where 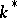 is the multiplicative group of
is the multiplicative group of 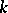 and
and
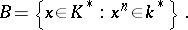 |
There exists a non-degenerate Kummer pairing, i.e. a mapping
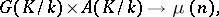 |
where 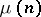 is the subgroup of
is the subgroup of 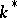 generated by
generated by 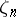 . If
. If 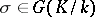 and
and 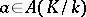 , the pairing is defined by the formula
, the pairing is defined by the formula 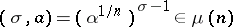 , where
, where 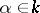 , and
, and 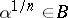 is some representative of the element
is some representative of the element  . The pairing defines a canonical isomorphism.
. The pairing defines a canonical isomorphism.
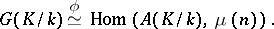 | (2) |
In other words, any automorphism 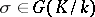 is defined by its action on the roots
is defined by its action on the roots 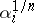 in (1), and this action may be arbitrary, provided that the roots
in (1), and this action may be arbitrary, provided that the roots 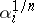 are independent. In particular, if
are independent. In particular, if 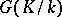 is a cyclic group, then
is a cyclic group, then 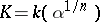 , where
, where 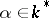 .
.
Let 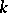 be a normal extension of a field
be a normal extension of a field 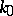 and let
and let 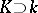 be a Kummer extension. Then the field
be a Kummer extension. Then the field 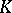 is normal over
is normal over 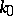 if and only if
if and only if 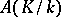 is mapped into itself by
is mapped into itself by 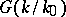 . In that case the isomorphism (2) is a
. In that case the isomorphism (2) is a 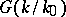 -isomorphism, i.e. if
-isomorphism, i.e. if 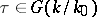 ,
, 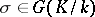 and if
and if
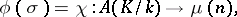 |
then 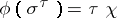 , where
, where 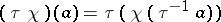 . (The group
. (The group 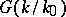 acts on
acts on 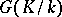 via conjugation in
via conjugation in 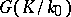 .) By the above proposition, many problems concerning Abelian extensions of exponent
.) By the above proposition, many problems concerning Abelian extensions of exponent  of a field
of a field 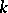 can be reduced to the theory of Kummer extensions even if
can be reduced to the theory of Kummer extensions even if  . To be precise: If
. To be precise: If 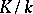 is such an extension, then
is such an extension, then 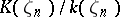 is a Kummer extension, and its Kummer group is characterized by the condition: If
is a Kummer extension, and its Kummer group is characterized by the condition: If 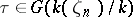 and
and  , then
, then 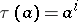 , where
, where 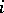 is a natural number which is defined modulo
is a natural number which is defined modulo  by the condition
by the condition 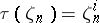 .
.
The main results concerning Kummer extensions may be derived as corollaries of the Hilbert theorem on cyclic extensions, according to which the one-dimensional Galois cohomology group 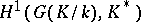 is trivial.
is trivial.
The theory of Kummer extensions carries over to the case of infinite Abelian extensions of exponent  . When this is done, the Kummer pairing establishes a Pontryagin duality between the profinite group
. When this is done, the Kummer pairing establishes a Pontryagin duality between the profinite group 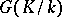 (endowed with the Krull topology) and the discrete group
(endowed with the Krull topology) and the discrete group 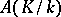 (see [1], [2]).
(see [1], [2]).
The theory of Kummer extensions, also known as Kummer theory, has an analogue in the case of extensions (1) with 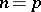 (Artin–Schreier theory). The role of the group
(Artin–Schreier theory). The role of the group 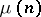 in that situation is played by the additive group of the prime subfield
in that situation is played by the additive group of the prime subfield 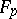 of
of 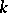 . The main result of the theory is: Any Abelian extension
. The main result of the theory is: Any Abelian extension 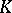 of exponent
of exponent 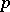 of a field
of a field 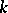 is of the form
is of the form 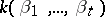 , where
, where 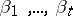 are roots of equations of the type
are roots of equations of the type 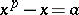 (see [1]). There is also a generalization of this theory, due to E. Witt, to the case
(see [1]). There is also a generalization of this theory, due to E. Witt, to the case 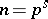 , where
, where 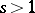 , using Witt vectors (cf. Witt vector).
, using Witt vectors (cf. Witt vector).
Finally, an attempt has been made to construct a non-Abelian "Kummer theory" [3], where the multiplicative group of the field is replaced by the matrix group 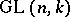 .
.
References
| [1] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [2] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1968) |
| [3] | S. Takahashi, "Generation of Galois extensions by matrix roots" J. Math. Soc. Japan , 20 : 1–2 (1968) pp. 365–370 |
Comments
The theory of Kummer extensions fits, of course, in the general framework of class field theory, cf. [a1] for details.
References
| [a1] | J. Neukirch, "Class field theory" , Springer (1986) pp. Chapt. 4, §4 |
Kummer extension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kummer_extension&oldid=15655