Krein space
Let 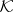 be a complex linear space on a which a Hermitian sesquilinear form
be a complex linear space on a which a Hermitian sesquilinear form 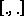 is defined (i.e. a mapping
is defined (i.e. a mapping 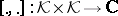 such that
such that 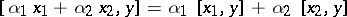 and
and 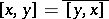 for all
for all 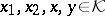 ,
, 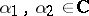 ). Then
). Then 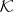 (or, more exactly,
(or, more exactly, 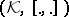 ) is called a Krein space if in
) is called a Krein space if in  there are two linear manifolds
there are two linear manifolds  such that
such that
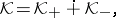 | (a1) |
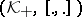 and
and 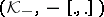 are Hilbert spaces (cf. Hilbert space) and
are Hilbert spaces (cf. Hilbert space) and  . It is always assumed that
. It is always assumed that 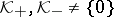 (otherwise
(otherwise 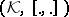 or
or 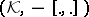 is a Hilbert space);
is a Hilbert space); 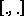 is called the indefinite inner product of the Krein space
is called the indefinite inner product of the Krein space 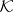 . If, in particular,
. If, in particular, 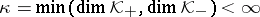 , then
, then  is a
is a 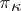 -space or Pontryagin space of index
-space or Pontryagin space of index 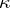 (cf. also Pontryagin space); in the sequel, for a
(cf. also Pontryagin space); in the sequel, for a 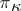 -space it is always assumed that
-space it is always assumed that 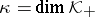 .
.
Using the decomposition (a1), on the Krein space 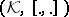 a Hilbert inner product
a Hilbert inner product 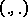 can be defined as follows:
can be defined as follows:
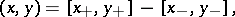 | (a2) |
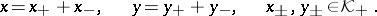 |
Although the decomposition (a1) is not unique, the decompositions of the components 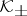 are uniquely determined and the Hilbert norms, generated by different decompositions (a1) according to (a2), are equivalent. All topological notions in a Krein space, if not stated explicitly otherwise, refer to this topology. In the Hilbert space
are uniquely determined and the Hilbert norms, generated by different decompositions (a1) according to (a2), are equivalent. All topological notions in a Krein space, if not stated explicitly otherwise, refer to this topology. In the Hilbert space  , the orthogonal projections onto
, the orthogonal projections onto 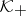 and
and 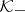 are denoted by
are denoted by 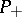 and
and 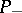 , respectively. Then for the operator
, respectively. Then for the operator 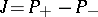 , called a fundamental symmetry, one has
, called a fundamental symmetry, one has
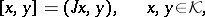 | (a3) |
and 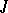 has the properties:
has the properties: 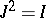 ,
, 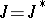 . Conversely, given a Hilbert space
. Conversely, given a Hilbert space 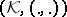 and in it an operator
and in it an operator 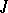 with these properties (or, more generally, an operator
with these properties (or, more generally, an operator 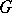 with
with  ,
, 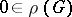 ), then an indefinite inner product is defined on
), then an indefinite inner product is defined on 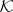 by (a3) (or, respectively, by the relation
by (a3) (or, respectively, by the relation
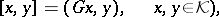 | (a4) |
and 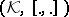 is a Krein space. Because of this construction, Krein spaces are sometimes called
is a Krein space. Because of this construction, Krein spaces are sometimes called  -spaces.
-spaces.
If, more generally, a Hilbert space 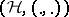 and a bounded self-adjoint, not semi-definite, operator
and a bounded self-adjoint, not semi-definite, operator 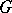 in
in 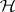 are given, the relation (a4) with
are given, the relation (a4) with 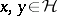 defines a Hermitian sesquilinear form
defines a Hermitian sesquilinear form 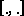 on
on 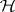 . This form can be extended by continuity to the completion of the quotient space
. This form can be extended by continuity to the completion of the quotient space  with respect to the norm
with respect to the norm 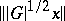 (
( ). This completion, equipped with
). This completion, equipped with 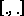 , is a Krein space containing
, is a Krein space containing 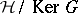 as a dense subset.
as a dense subset.
If  is a real and locally summable function on
is a real and locally summable function on 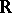 which assumes positive and negative values on sets of positive Lebesgue measure, then the space
which assumes positive and negative values on sets of positive Lebesgue measure, then the space 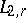 of all (classes of) measurable functions (cf. Measurable function)
of all (classes of) measurable functions (cf. Measurable function) 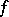 on
on  such that
such that 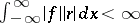 and equipped with the indefinite inner product
and equipped with the indefinite inner product 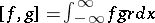 (
(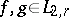 ) is a Krein space. More generally, if
) is a Krein space. More generally, if 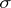 is a real function which is locally of bounded variation and not isotone on
is a real function which is locally of bounded variation and not isotone on 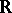 and
and 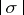 denotes its total variation, then the space
denotes its total variation, then the space 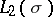 , of all measurable functions
, of all measurable functions 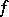 such that
such that 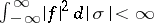 and equipped with the indefinite inner product
and equipped with the indefinite inner product 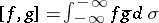 (
(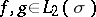 ) is a Krein space.
) is a Krein space.
Further, a complex linear space with a Hermitian sesquilinear form 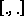 , which has
, which has 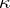 negative squares (that is, each linear manifold
negative squares (that is, each linear manifold 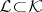 with
with 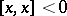 for
for 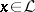 ,
, 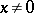 , is of dimension
, is of dimension 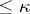 and at least one such manifold is of dimension
and at least one such manifold is of dimension 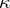 ), can be canonically imbedded into a
), can be canonically imbedded into a 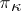 -space by taking a quotient space and completing it (see [a4], [a2], [a9], [a11]).
-space by taking a quotient space and completing it (see [a4], [a2], [a9], [a11]).
The indefinite inner product 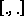 on the Krein space
on the Krein space 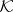 gives rise to a classification of the elements of
gives rise to a classification of the elements of  :
: 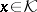 is called positive, non-negative, neutral, etc. if
is called positive, non-negative, neutral, etc. if 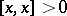 ,
,  ,
, 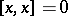 , etc. A linear manifold or a subspace
, etc. A linear manifold or a subspace 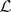 in
in 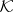 is called positive, non-negative, neutral, etc. if all its non-zero elements are positive, non-negative, neutral, etc. The set of all, e.g., non-negative elements is not linear, but it contains subspaces, and among them maximal ones, called maximal non-negative subspaces. All maximal non-negative subspaces of the Krein space
is called positive, non-negative, neutral, etc. if all its non-zero elements are positive, non-negative, neutral, etc. The set of all, e.g., non-negative elements is not linear, but it contains subspaces, and among them maximal ones, called maximal non-negative subspaces. All maximal non-negative subspaces of the Krein space 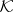 have the same dimension (as
have the same dimension (as  ). A subspace
). A subspace 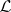 of
of 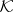 (with the decomposition (a1)) is maximal non-negative if and only if it can be written as
(with the decomposition (a1)) is maximal non-negative if and only if it can be written as 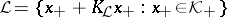 , where
, where 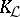 , the angular operator of
, the angular operator of 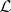 , is a contraction from
, is a contraction from 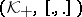 into
into 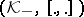 . A dual pair
. A dual pair 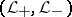 of subspaces of
of subspaces of 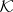 is defined as follows:
is defined as follows: 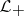 is a non-negative subspace,
is a non-negative subspace, 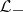 is a non-positive subspace and
is a non-positive subspace and 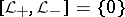 . Any dual pairs is contained in a maximal dual pair (maximality of dual pairs is defined in a natural way by inclusion); in a maximal dual pair
. Any dual pairs is contained in a maximal dual pair (maximality of dual pairs is defined in a natural way by inclusion); in a maximal dual pair 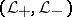 the subspace
the subspace 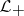 (respectively,
(respectively, 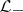 ) is maximal non-negative (respectively, non-positive) (R.S. Phillips).
) is maximal non-negative (respectively, non-positive) (R.S. Phillips).
Using the indefinite inner product, orthogonality can be defined in 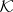 :
: 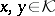 are called orthogonal if
are called orthogonal if  ; if
; if 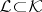 , then
, then 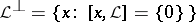 . Some properties of orthogonality in a Hilbert space are preserved; however, there are also essential differences; e.g.,
. Some properties of orthogonality in a Hilbert space are preserved; however, there are also essential differences; e.g., 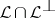 can contain non-zero vectors;
can contain non-zero vectors; 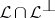 coincides with
coincides with  if
if  is neutral, and
is neutral, and 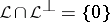 is equivalent to
is equivalent to 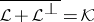 .
.
For a densely-defined linear operator 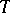 in the Krein space
in the Krein space 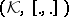 an adjoint
an adjoint 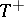 (sometimes called
(sometimes called 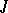 -adjoint) is defined by
-adjoint) is defined by 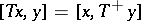 (
(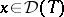 ,
, 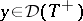 ). If
). If 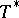 denotes the adjoint of
denotes the adjoint of 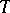 in the Hilbert space
in the Hilbert space 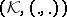 (see (a2)), then evidently
(see (a2)), then evidently 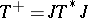 . Now in the Krein space
. Now in the Krein space  classes of operators are defined more or less similarly to the case of a Hilbert space:
classes of operators are defined more or less similarly to the case of a Hilbert space: 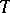 is symmetric if
is symmetric if 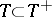 , self-adjoint if
, self-adjoint if 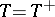 , dissipative if
, dissipative if 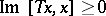 (
( ), contractive if
), contractive if 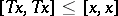 (
(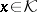 ), unitary if
), unitary if 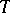 is bounded,
is bounded, 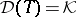 and
and 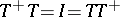 , etc. Also, new classes of operators arise: E.g.,
, etc. Also, new classes of operators arise: E.g., 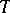 is a plus-operator if
is a plus-operator if 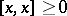 implies
implies 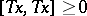 , and a doubly plus-operator if
, and a doubly plus-operator if 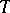 and
and 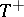 are plus-operators. In a Krein space a densely-defined isometric operator
are plus-operators. In a Krein space a densely-defined isometric operator 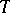 (i.e.
(i.e. 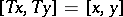 for all
for all 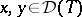 ) need not be continuous. As in a Hilbert space, self-adjoint and unitary, symmetric and isometric, dissipative and contractive operators are related by the Cayley transform. E.g., if
) need not be continuous. As in a Hilbert space, self-adjoint and unitary, symmetric and isometric, dissipative and contractive operators are related by the Cayley transform. E.g., if 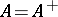 ,
, 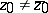 and
and 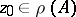 , then
, then 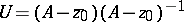 is unitary.
is unitary.
The spectrum of a self-adjoint operator 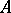 in a Krein space is not necessarily real (it can even cover the whole plane), but it is symmetric with respect to the real axis. Similarly, the spectrum of a unitary operator is symmetric with respect to the unit circle.
in a Krein space is not necessarily real (it can even cover the whole plane), but it is symmetric with respect to the real axis. Similarly, the spectrum of a unitary operator is symmetric with respect to the unit circle.
The indefinite inner product sometimes gives a classification of the points of the spectrum of an operator: An eigen value is said to be of positive type (negative type, etc.) if the corresponding eigen space is positive (negative, etc.).
If  ,
, 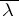 are isolated eigen values of the self-adjoint operator
are isolated eigen values of the self-adjoint operator 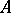 in a Krein space, then for the corresponding Riesz projections
in a Krein space, then for the corresponding Riesz projections 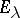 ,
, 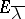 one has
one has 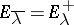 , and if, e.g.,
, and if, e.g., 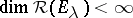 , then the restrictions
, then the restrictions 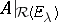 and
and 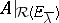 have the same Jordan structure. If in a
have the same Jordan structure. If in a 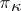 -space the symmetric operator
-space the symmetric operator 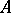 has a real non-semi-simple eigen value
has a real non-semi-simple eigen value 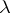 , then the corresponding algebraic eigen space
, then the corresponding algebraic eigen space 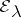 can be decomposed into a direct orthogonal sum:
can be decomposed into a direct orthogonal sum: 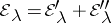 , where
, where 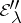 is a positive subspace contained in the geometric eigen space of
is a positive subspace contained in the geometric eigen space of 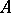 at
at 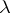 , and
, and 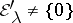 is invariant under
is invariant under 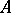 with
with 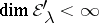 ; if
; if 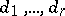 are the lengths of the Jordan chains of
are the lengths of the Jordan chains of  , one puts
, one puts 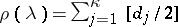 ; if
; if  is a non-real eigen value of
is a non-real eigen value of 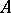 , one defines
, one defines 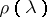 as the dimension of the corresponding algebraic eigen space. Then
as the dimension of the corresponding algebraic eigen space. Then 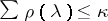 , where the sum extends over all eigen values
, where the sum extends over all eigen values 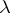 of
of 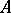 in the closed upper half-plane. In particular, the length of any Jordan chain of
in the closed upper half-plane. In particular, the length of any Jordan chain of  is
is 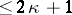 , and the number of eigen values of
, and the number of eigen values of 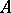 in the open upper half-plane, and also the number of non-semi-simple eigen values of
in the open upper half-plane, and also the number of non-semi-simple eigen values of 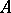 , does not exceed
, does not exceed 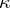 .
.
Specific results for Krein spaces are statements about the existence of maximal non-negative (or maximal non-positive) subspaces, which are invariant under a given operator. The first general result of this type was proved by L.S. Pontryagin in 1944, stating that a self-adjoint operator in a 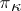 -space has a
-space has a 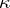 -dimensional non-positive (that is, a maximal non-positive) invariant subspace. Subsequently, similar results were proved for various classes of operators in Krein spaces. E.g., a bounded linear operator
-dimensional non-positive (that is, a maximal non-positive) invariant subspace. Subsequently, similar results were proved for various classes of operators in Krein spaces. E.g., a bounded linear operator 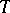 in a Krein space has a maximal non-negative invariant subspace if
in a Krein space has a maximal non-negative invariant subspace if  is compact and, additionally,
is compact and, additionally, 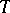 is self-adjoint or dissipative or unitary or a plus-operator, etc. (see [a2], [a4]). One possibility for proving these results, e.g. for a unitary operator
is self-adjoint or dissipative or unitary or a plus-operator, etc. (see [a2], [a4]). One possibility for proving these results, e.g. for a unitary operator 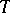 , is to establish the existence of a fixed point
, is to establish the existence of a fixed point 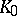 of the fractional-linear transformation
of the fractional-linear transformation
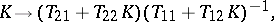 |
where 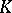 is a contraction from
is a contraction from 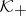 into
into 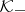 (an angular operator) and
(an angular operator) and 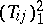 is the matrix representation of
is the matrix representation of 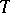 with respect to (a1). By different methods also in other cases the existence of a maximal non-negative invariant subspace has been proved, e.g.: 1)
with respect to (a1). By different methods also in other cases the existence of a maximal non-negative invariant subspace has been proved, e.g.: 1) 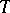 is unitary and
is unitary and 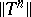 is uniformly bounded for all
is uniformly bounded for all 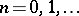 ; 2)
; 2) 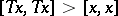 for all
for all 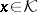 ,
, 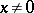 , and
, and 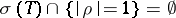 ; and 3)
; and 3) 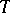 is bounded, self-adjoint and there exists a polynomial
is bounded, self-adjoint and there exists a polynomial 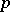 such that
such that 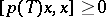 (
(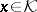 ). In many cases these maximal non-positive invariant subspaces
). In many cases these maximal non-positive invariant subspaces 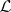 can be specified by properties of the spectrum of
can be specified by properties of the spectrum of 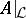 . E.g., if
. E.g., if 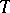 is bounded, self-adjoint and
is bounded, self-adjoint and 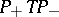 is compact, then
is compact, then 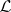 can be chosen such that
can be chosen such that 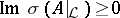 . There are also results about the existence of a common invariant maximal non-positive subspace for a commuting family of operators, e.g.: A commuting family of bounded self-adjoint operators in a
. There are also results about the existence of a common invariant maximal non-positive subspace for a commuting family of operators, e.g.: A commuting family of bounded self-adjoint operators in a  -space has a common maximal non-negative invariant subspace (M.A. Naimark; for applications in the representation theory of groups in
-space has a common maximal non-negative invariant subspace (M.A. Naimark; for applications in the representation theory of groups in 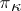 -spaces see [a19]). Phillips asked ([a16]) if a dual pair of subspaces of
-spaces see [a19]). Phillips asked ([a16]) if a dual pair of subspaces of  which are invariant under a commutative algebra
which are invariant under a commutative algebra  of bounded self-adjoint operators in the Krein space
of bounded self-adjoint operators in the Krein space 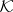 can always be extended to a maximal dual pair whose subspaces are still invariant under
can always be extended to a maximal dual pair whose subspaces are still invariant under 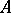 (which would imply that each bounded self-adjoint operator in
(which would imply that each bounded self-adjoint operator in 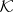 has a maximal non-negative invariant subspace). Only partial solutions to this problem are known (cf. [a4], [a2], [a14]).
has a maximal non-negative invariant subspace). Only partial solutions to this problem are known (cf. [a4], [a2], [a14]).
A self-adjoint operator 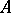 in the Krein space
in the Krein space 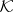 is called definitizable (positizable in [a4]) if
is called definitizable (positizable in [a4]) if 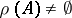 and if there exists a polynomial
and if there exists a polynomial 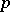 such that
such that 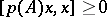 (
(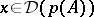 ). Each self-adjoint operator
). Each self-adjoint operator 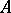 in a
in a 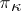 -space has this property (where
-space has this property (where 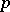 can be chosen to be
can be chosen to be 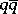 with
with 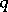 the minimal polynomial of
the minimal polynomial of 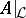 ,
,  being a
being a 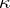 -dimensional non-positive invariant subspace of
-dimensional non-positive invariant subspace of 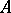 ); also, each self-adjoint operator
); also, each self-adjoint operator 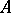 in a Krein space for which
in a Krein space for which 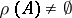 and for which the Hermitian sesquilinear form
and for which the Hermitian sesquilinear form 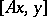 (
(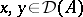 ) has a finite number of negative squares, is definitizable.
) has a finite number of negative squares, is definitizable.
The non-real spectrum  of the definitizable operator
of the definitizable operator 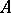 consists of at most finitely many eigen values, and
consists of at most finitely many eigen values, and 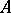 has a spectral function, with possibly certain critical points [a13], [a2]. This means that there is a finite set
has a spectral function, with possibly certain critical points [a13], [a2]. This means that there is a finite set 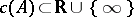 (of critical points) such that on the semi-ring
(of critical points) such that on the semi-ring  , consisting of all bounded intervals of
, consisting of all bounded intervals of 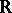 with end points not in
with end points not in 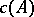 and their complements, a homomorphism
and their complements, a homomorphism 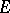 with values in the set of all self-adjoint projections in the Krein space
with values in the set of all self-adjoint projections in the Krein space 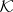 is defined, such that for
is defined, such that for 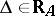 : a)
: a) 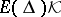 is a positive (negative) subspace if
is a positive (negative) subspace if 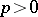 (respectively,
(respectively, 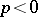 ) on
) on 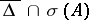 for some definitizing polynomial
for some definitizing polynomial 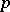 of
of 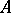 ; b)
; b) 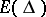 is in the double commutant of the resolvent of
is in the double commutant of the resolvent of 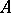 ; and c) if
; and c) if 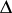 is bounded, then
is bounded, then 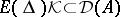 and
and 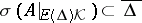 ,
, 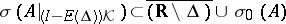 . If, in particular,
. If, in particular, 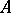 is bounded and
is bounded and 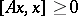 (
(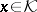 ), then
), then 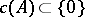 , and one has
, and one has
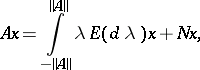 |
for some bounded operator  such that
such that 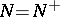 ,
, 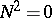 ,
, 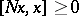 (
(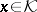 ).
).
If the spectrum of a definitizable operator 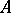 is discrete, then the linear span of its algebraic eigen spaces is dense in
is discrete, then the linear span of its algebraic eigen spaces is dense in 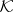 ; if
; if 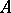 is compact and self-adjoint in a
is compact and self-adjoint in a  -space
-space 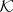 and
and 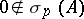 , then there is a Riesz basis of
, then there is a Riesz basis of 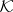 consisting of eigen and associated vectors of
consisting of eigen and associated vectors of 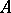 (I.S. Iokhvidov).
(I.S. Iokhvidov).
There is a theory of extensions of symmetric operators to self-adjoint operators and of generalized resolvents in 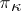 -spaces, and also in Krein spaces, which is similar to the Hilbert space situation. The same is true for dilation theory: Each bounded linear operator
-spaces, and also in Krein spaces, which is similar to the Hilbert space situation. The same is true for dilation theory: Each bounded linear operator 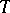 in a Krein space
in a Krein space 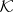 has a unitary dilation
has a unitary dilation 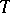 in some Krein space
in some Krein space 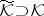 ([a2]). In this context one has the following result: Let
([a2]). In this context one has the following result: Let 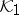 ,
, 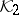 be Krein spaces,
be Krein spaces, 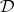 a simply-connected open domain with smooth boundary such that
a simply-connected open domain with smooth boundary such that 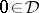 ,
, 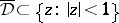 , and let
, and let 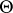 be a function which is holomorphic in
be a function which is holomorphic in 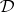 whose values are bounded linear operators from
whose values are bounded linear operators from 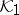 to
to 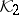 . Then there exists a Krein space
. Then there exists a Krein space 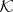 and a unitary operator
and a unitary operator
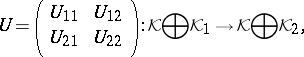 |
such that
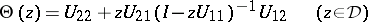 |
(T.Ya. Azizov, see [a2], [a6]; here unitary means that 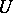 maps the Krein space
maps the Krein space 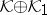 continuously onto the Krein space
continuously onto the Krein space 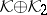 , preserving the indefinite inner product).
, preserving the indefinite inner product).
Some of the first papers about Krein spaces or, more generally, spaces with indefinite inner product, were stimulated by problems of (quantum) mechanics ([a4], [a2]; see also [a18], [a17]). Operators in Krein spaces arise also in a natural way in problems in mathematical analysis. Some examples of these are: I) Consider the canonical system of differential equations 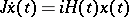 on
on 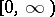 , where
, where 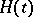 ,
, 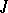 are
are 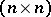 matrices,
matrices, 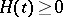 ,
, 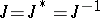 , and let
, and let 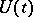 be the corresponding matrizant (cf. Cauchy operator):
be the corresponding matrizant (cf. Cauchy operator): 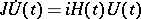 ,
, 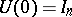 . Then
. Then 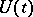 is
is 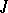 -unitary (that is, unitary with respect to the inner product defined in
-unitary (that is, unitary with respect to the inner product defined in 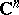 by the matrix
by the matrix 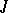 , see (a3)), and, e.g., in the stability theory for periodic equations
, see (a3)), and, e.g., in the stability theory for periodic equations 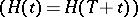 the classification of the eigen values of
the classification of the eigen values of 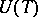 into those of positive or negative type plays an essential role ([a5], [a8]). II) The integral operator
into those of positive or negative type plays an essential role ([a5], [a8]). II) The integral operator 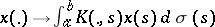 ,
, 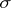 real and of bounded variation on the interval
real and of bounded variation on the interval 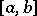 ,
, 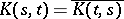 (
(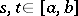 ), is self-adjoint in the Krein space
), is self-adjoint in the Krein space 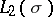 . III) The theory of dual pairs of subspaces of a Krein space and their extensions to maximal dual pairs is related to certain questions in the theory of extensions of dissipative operators in a Hilbert space to maximal dissipative ones. Phillips started these investigations in connection with the Cauchy problem for dissipative hyperbolic and parabolic systems (see [a2], [a4] for references). IV) With the monic operator polynomial
. III) The theory of dual pairs of subspaces of a Krein space and their extensions to maximal dual pairs is related to certain questions in the theory of extensions of dissipative operators in a Hilbert space to maximal dissipative ones. Phillips started these investigations in connection with the Cauchy problem for dissipative hyperbolic and parabolic systems (see [a2], [a4] for references). IV) With the monic operator polynomial 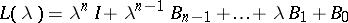 ,
, 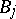 bounded self-adjoint operators in some Hilbert space
bounded self-adjoint operators in some Hilbert space 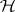 , one can associate the so-called companion operator
, one can associate the so-called companion operator
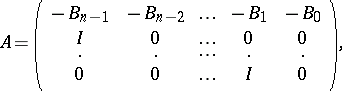 |
which is self-adjoint in the Krein space 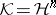 ,
, 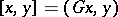 (
( ), where
), where 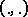 is the inner product in
is the inner product in 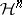 and
and
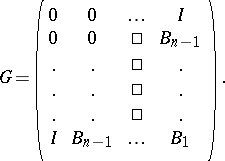 |
If, e.g.,  and
and 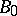 is compact and
is compact and 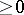 , the results about the existence of maximal non-negative invariant subspaces mentioned above imply that there exists a bounded linear operator
, the results about the existence of maximal non-negative invariant subspaces mentioned above imply that there exists a bounded linear operator 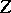 in
in 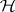 satisfying
satisfying 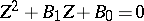 ,
, 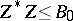 and
and 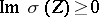 [a12]. In a similar way, if
[a12]. In a similar way, if 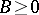 ,
, 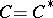 and
and 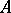 are
are 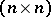 matrices such that
matrices such that  has
has  positive and
positive and  negative eigen values, the solutions
negative eigen values, the solutions 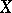 of the matrix Riccati equation
of the matrix Riccati equation
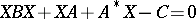 |
with 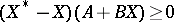 are in bijective correspondence with all maximal non-positive subspaces which are invariant under the self-adjoint operator
are in bijective correspondence with all maximal non-positive subspaces which are invariant under the self-adjoint operator 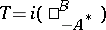 in the
in the 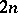 -dimensional Krein space
-dimensional Krein space 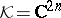 , equipped with the indefinite inner product (a4) (see [a8]). V) If
, equipped with the indefinite inner product (a4) (see [a8]). V) If 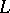 is a formally-symmetric regular ordinary differential operator on the interval
is a formally-symmetric regular ordinary differential operator on the interval 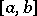 with symmetric boundary conditions at
with symmetric boundary conditions at  and
and 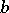 , and
, and  is a summable function on
is a summable function on 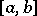 which is not of constant sign (a.e.) on
which is not of constant sign (a.e.) on 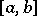 , then the differential equation
, then the differential equation 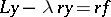 leads to a self-adjoint operator
leads to a self-adjoint operator 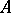 in the Krein space
in the Krein space 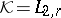 with inner product
with inner product 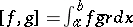 . If
. If 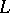 is semi-bounded from below, the operator
is semi-bounded from below, the operator 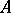 is definitizable. VI) Krein spaces can be associated with certain eigen value problems for ordinary differential operators containing the eigen value parameters in the boundary conditions. E.g., consider in
is definitizable. VI) Krein spaces can be associated with certain eigen value problems for ordinary differential operators containing the eigen value parameters in the boundary conditions. E.g., consider in 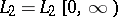 the problem
the problem
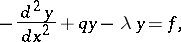 |
which is supposed to have a limit point at 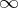 and with a boundary condition
and with a boundary condition 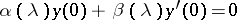 at
at 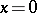 (
(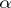 ,
, 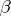 are functions which are holomorphic on some set
are functions which are holomorphic on some set 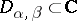 and satisfying a symmetry condition). The solution of this problem can be represented as
and satisfying a symmetry condition). The solution of this problem can be represented as 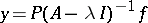 (
(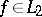 ), where, in general,
), where, in general, 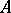 is a self-adjoint operator in some Krein space
is a self-adjoint operator in some Krein space 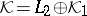 and
and 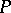 is the orthogonal projection from
is the orthogonal projection from 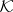 onto
onto 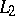 [a17]. VII) Certain classes of analytic functions are closely related to the theory of operators in
[a17]. VII) Certain classes of analytic functions are closely related to the theory of operators in 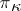 -spaces. This concerns, e.g., functions
-spaces. This concerns, e.g., functions 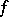 which are defined and meromorphic in the upper half-plane (or the unit disc) and which are such that the kernel
which are defined and meromorphic in the upper half-plane (or the unit disc) and which are such that the kernel
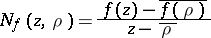 |
(or
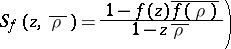 |
has 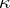 negative squares (that is, for arbitrary
negative squares (that is, for arbitrary  and
and  , the matrix
, the matrix 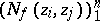 has at most
has at most  negative eigen values and for at least one choice of
negative eigen values and for at least one choice of 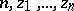 it has
it has 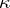 negative eigen values). Corresponding extrapolation or moment problems can be treated by making use of results of the theory of symmetric or isometric operators in
negative eigen values). Corresponding extrapolation or moment problems can be treated by making use of results of the theory of symmetric or isometric operators in 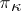 -spaces (see [a12], [a2]).
-spaces (see [a12], [a2]).
References
| [a1] | T.Ya Azizov, I.S. Iokhvidov, "Linear operators in spaces with indefinite metric and their applications" Russian Math. Surveys , 15 (1981) pp. 438–490 Itogi Nauk. i Tekhn. Mat. Anal. , 17 (1979) pp. 113–205 |
| [a2] | T.Ya Azizov, I.S. Iokhvidov, "Foundations of the theory of linear operators in spaces with indefinite metric" , Moscow (1986) (In Russian) |
| [a3] | T. Ando, "Linear operators in Krein spaces" , Hokkaido Univ. (1979) |
| [a4] | J. Bognár, "Indefinite inner product spaces" , Springer (1974) |
| [a5] | Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [a6] | A. Dijksma, H. Langer, H.S.V. de Snoo, "Unitary colligations in Krein spaces and their role in the extension theory of isometries and symmetric linear relations in Hilbert spaces" S. Kurepa (ed.) et al. (ed.) , Foundational analysis II , Lect. notes in math. , 1247 , Springer (1987) pp. 1–42 |
| [a7] | A. Dijksma, H. Langer, H.S.V. de Snoo, "Symmetric Sturm–Liouville operators with eigenvalues depending boundary conditions" , Oscillation, Bifurcations and Chaos , CMS Conf. Proc. , 8 , Amer. Math. Soc. (1987) pp. 87–116 |
| [a8] | I. [I. Gokhberg] Gohberg, P. Lancaster, L. Rodman, "Matrices and indefinite scalar products" , Birkhäuser (1983) |
| [a9] | I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982) |
| [a10] | V.I. Istraţescu, "Inner product spaces. Theory and applications" , Reidel (1987) |
| [a11] | M.G. Krein, "Introduction to the geometry of indefinite 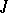 -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) |
| [a12] | M.G. Krein, H. Langer, "Ueber einige Fortsetzungsprobleme, die eng mit der Theorie hermitescher Operatoren im Raume 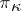 zusammenhängen, I: Einige Funktionenklassen und ihre Darstellungen" Math. Nachr. , 77 (1977) pp. 187–236 zusammenhängen, I: Einige Funktionenklassen und ihre Darstellungen" Math. Nachr. , 77 (1977) pp. 187–236 |
| [a13] | H. Langer, "Spectral functions of definitizable operators in Krein spaces" D. Butković (ed.) et al. (ed.) , Functional analysis , Lect. notes in math. , 948 , Springer (1982) pp. 1–46 |
| [a14] | H. Langer, "Invariante Teilräume definisierbarer 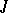 -selbstadjungierter Operatoren" Ann. Acad. Sci. Fenn A. I , 475 (1971) -selbstadjungierter Operatoren" Ann. Acad. Sci. Fenn A. I , 475 (1971) |
| [a15] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) |
| [a16] | R.S. Phillips, "The extensions of dual subspaces invariant under an algebra" , Proc. Internat. Symp. Linear Spaces (Jerusalem, 1960) , Pergamon (1961) pp. 366–398 |
| [a17] | L. Bracci, G. Morchio, F. Strocchi, "Wigner's theorem on symmetries in indefinite metric spaces" Comm. Math. Phys. , 41 (1975) pp. 289–299 |
| [a18] | K.L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966) |
| [a19] | M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in a space with indefinite metric" Itogi Nauk. i Tekhn. Mat. Anal. (1969) pp. 73–105 (In Russian) |
| [a20] | M.G. Krein, H. Langer, "On some mathematical principles in the linear theory of damped oscillations of continua" Integral Equations, Operator Theory , 1 (1978) pp. 364–399; 539–566 Proc. Internat. Symp. Appl. Theory of Functions in Continuum Mechanics, Tbilizi , 2 (1963) pp. 283–322 |
Krein space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Krein_space&oldid=18988