Kernel of a morphism in a category

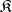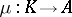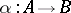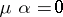A concept generalizing that of the kernel of a linear transformation of vector spaces, the kernel of a homomorphism of groups, rings, etc. Let be a category with null (or zero) morphisms. A morphism is called a kernel of a morphism if and if every morphism for which 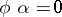can be uniquely represented as 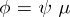. A kernel of a morphism 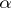is denoted by .

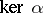If 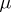and 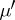are both kernels of 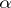, then 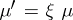for a unique isomorphism 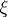. Conversely, if 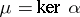and if 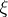is an isomorphism, then 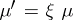is a kernel of 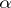. Thus, the kernels of a morphism 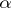form a subobject of 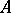, denoted by .

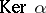If 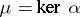, then 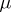is a monomorphism. In general, the converse is not true; a monomorphism which occurs as a kernel is called a normal monomorphism. The kernel of the null morphism is the identity morphism 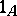. The kernel of 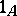exists if and only if 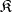contains a null object (cf. Null object of a category).

Kernels do not always exist in a category with null morphisms. On the other hand, in a category 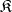with a null object a morphism 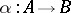has a kernel if and only if a pullback of 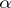and exists in .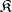

The concept of the "kernel of a morphism" is the dual to that of the "cokernel of a morphism" .

Comments

The concept "kernel of a pair of morphismskernel of a pair of morphisms" (not to be confused with "kernel pair of a morphism" ) is also frequently used. In English, the usual name for this concept is an equalizer. An equalizer of a parallel pair of morphism 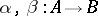is a morphism 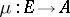such that 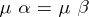and such that every 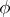satisfying 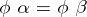factors uniquely through 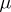. Kernels are a special case of equalizers: 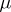is a kernel of 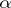if and only if it is an equalizer of 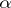and . 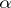Conversely, in an additive category an equalizer of and 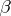is the same thing as a kernel of 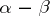; but in general the notion of equalizer is more widely applicable, since it does not require the existence of null morphisms. A monomorphism which occurs as an equalizer is called a regular monomorphism.

References

[a1]	B. Mitchell, "Theory of categories" , Acad. Press (1965)
[a2]	J. Adámek, "Theory of mathematical structures" , Reidel (1983)