Kantorovich process
An iterative method for improving the approximation to the value of a root of a non-linear functional (operator) equation (a generalization of Newton's method cf. Newton method). For the equation  , where
, where  is a non-linear operator from one Banach space to another, the formula for calculating the root has the form
is a non-linear operator from one Banach space to another, the formula for calculating the root has the form
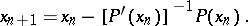 |
(Here  is the Fréchet derivative.) Sometimes a modified process, given by the following formula, is used:
is the Fréchet derivative.) Sometimes a modified process, given by the following formula, is used:
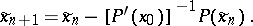 |
Suppose that the operator  is twice continuously differentiable and that the following conditions hold (see [2]):
is twice continuously differentiable and that the following conditions hold (see [2]):
1) the linear operator  exists;
exists;
2)  ;
;
3)  when
when 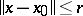 ;
;
4) 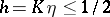 ;
;
5) 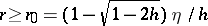 .
.
Then the equation 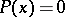 has a solution
has a solution 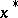 such that
such that
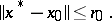 |
The sequences 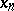 and
and 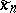 converge to this solution, with
converge to this solution, with
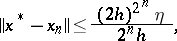 |
and in the case 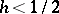 ,
,
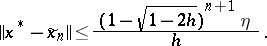 |
The Kantorovich process always converges to a root 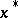 of the equation
of the equation 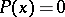 , provided that
, provided that 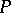 is sufficiently smooth,
is sufficiently smooth,  exists and the initial approximation
exists and the initial approximation 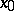 is chosen sufficiently close to
is chosen sufficiently close to 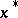 . If
. If 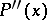 exists and is continuous, then the convergence of the basic process is quadratic. The rate of convergence of the modified process is that of a decreasing geometric progression; the denominator of this progression tends to zero as
exists and is continuous, then the convergence of the basic process is quadratic. The rate of convergence of the modified process is that of a decreasing geometric progression; the denominator of this progression tends to zero as 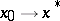 .
.
The process was proposed by L.V. Kantorovich [1].
References
| [1] | L.V. Kantorovich, "On Newton's method for functional equations" Dokl. Akad. Nauk SSSR , 59 : 6 (1948) pp. 1237–1240 (In Russian) |
| [2] | L.V. Kantorovich, G.P. Akilov, "Functional analysis in normed spaces" , Pergamon (1964) (Translated from Russian) |
| [3] | M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
| [4] | L. Collatz, "Funktionalanalysis und numerische Mathematik" , Springer (1964) |
Comments
The modified process is also called the Newton–Raphson method.
References
| [a1] | J.E. Denis jr., R. Schnable, "Numerical methods for unconstrained optimization and nonlinear equations" , Prentice-Hall (1983) |
| [a2] | J.M. Ortega, W.C. Rheinboldt, "Iterative solution of non-linear equations in several variables" , Acad. Press (1970) |
Kantorovich process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kantorovich_process&oldid=14866