K-system(2)

A measurable flow ( -flow) or cascade (
-flow) or cascade ( -cascade) in a Lebesgue space such that there is a measurable partition (cf. Measurable decomposition)
-cascade) in a Lebesgue space such that there is a measurable partition (cf. Measurable decomposition)  of the phase space with the following properties: a) it is increasing (formerly called invariant) with respect to
of the phase space with the following properties: a) it is increasing (formerly called invariant) with respect to  , that is,
, that is,  is a refinement
is a refinement 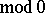 of
of 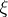 when
when 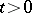 ; b) it is a two-sided generator for
; b) it is a two-sided generator for 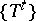 , that is, the only measurable partition
, that is, the only measurable partition 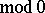 that is finer
that is finer 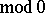 than all the
than all the 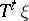 is the partition into points; and c) the only measurable partition
is the partition into points; and c) the only measurable partition  that is coarser
that is coarser 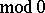 than all the
than all the 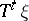 is the trivial partition, whose only element is the whole phase space.
is the trivial partition, whose only element is the whole phase space.
An automorphism of a measure space whose iterations form a  -cascade is called a
-cascade is called a 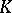 -automorphism. If
-automorphism. If 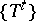 is a
is a 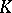 -system, then all
-system, then all 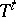 with
with 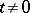 are
are 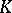 -automorphisms. Conversely, given a measurable flow or cascade
-automorphisms. Conversely, given a measurable flow or cascade  , if just one
, if just one 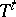 is a
is a 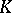 -automorphism, then
-automorphism, then 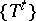 is a
is a 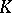 -system.
-system. 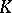 -systems posses strong ergodic properties: positive entropy (cf. Entropy theory of a dynamical system) and ergodicity; mixing of all degrees and they have a countably-multiple Lebesgue spectrum (see Spectrum of a dynamical system; and also [2]).
-systems posses strong ergodic properties: positive entropy (cf. Entropy theory of a dynamical system) and ergodicity; mixing of all degrees and they have a countably-multiple Lebesgue spectrum (see Spectrum of a dynamical system; and also [2]).
An endomorphism of a Lebesgue space has completely-positive entropy if all its non-trivial quotient endomorphisms have positive entropy. Among these are the 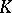 -automorphisms (namely, they are just the automorphisms with completely-positive entropy) and also other interesting objects (exact endomorphisms; cf. Exact endomorphism). The notion of a
-automorphisms (namely, they are just the automorphisms with completely-positive entropy) and also other interesting objects (exact endomorphisms; cf. Exact endomorphism). The notion of a  -system can be generalized in other directions: to the case of an infinite invariant measure (see [6], [7], [11]) and for the action of groups other than
-system can be generalized in other directions: to the case of an infinite invariant measure (see [6], [7], [11]) and for the action of groups other than 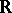 and
and 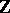 (see [8]–[10], [12]).
(see [8]–[10], [12]).
 -systems are sometimes called Kolmogorov systems (flows, etc.), after their originator (see ), who used the term "quasi-regular dynamical systemquasi-regular" . This emphasizes the analogy with regular random processes (see [4]). If a random process
-systems are sometimes called Kolmogorov systems (flows, etc.), after their originator (see ), who used the term "quasi-regular dynamical systemquasi-regular" . This emphasizes the analogy with regular random processes (see [4]). If a random process 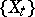 , stationary in the narrow sense of the word, is interpreted as a dynamical system, then the values of the process "in the past" define a certain increasing measurable partition
, stationary in the narrow sense of the word, is interpreted as a dynamical system, then the values of the process "in the past" define a certain increasing measurable partition  , which is the smallest with respect to which all the
, which is the smallest with respect to which all the  with
with 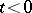 are measurable. If
are measurable. If 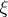 has the properties b) and c) above (the "all or nothing" law), then the process is called regular. In particular, this probabilistic form presents the simplest example of a
has the properties b) and c) above (the "all or nothing" law), then the process is called regular. In particular, this probabilistic form presents the simplest example of a 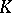 -automorphism: a Bernoulli automorphism.
-automorphism: a Bernoulli automorphism.
Given a measurable flow or cascade in a Lebesgue space, if one of the 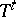 is isomorphic to a Bernoulli automorphism, then they all are (when
is isomorphic to a Bernoulli automorphism, then they all are (when 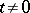 ). In this case the dynamical system is called Bernoullian (see [5]). There are
). In this case the dynamical system is called Bernoullian (see [5]). There are  -systems that are not Bernoullian.
-systems that are not Bernoullian. 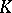 -systems (even Bernoullian ones) arise naturally not only in probability theory, but also in problems of an algebraic, geometric and even physical nature (see [2], [3], [5], [13], [14]).
-systems (even Bernoullian ones) arise naturally not only in probability theory, but also in problems of an algebraic, geometric and even physical nature (see [2], [3], [5], [13], [14]).
References
| [1a] | A.N. Kolmogorov, "A new metric invariant of transitive dynamical systems and of endomorphisms of Lebesgue spaces" Dokl. Akad. Nauk SSSR , 119 : 5 (1958) pp. 861–864 (In Russian) |
| [1b] | A.N. Kolmogorov, "On the entropy as a metric invariant of automorphisms" Dokl. Akad. Nauk SSSR , 124 : 4 (1959) pp. 754–755 (In Russian) |
| [2] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian) |
| [3] | A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" J. Soviet Math. , 7 (1977) pp. 974–1065 Itogi Nauk i Tekhn. Mat. Anal. , 13 (1975) pp. 129–262 |
| [4] | Yu.A. Rozanov, "Stationary random processes" , Holden-Day (1967) (Translated from Russian) |
| [5] | D. Ornstein, "Ergodic theory, randomness, and dynamical systems" , Yale Univ. Press (1974) |
| [6] | W. Parry, "Ergodic and spectral analysis of certain infinite measure preserving transformations" Proc. Amer. Math. Soc. , 16 : 5 (1965) pp. 960–966 |
| [7] | J.K. Dugdale, "Kolmogorov automorphisms in 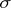 -finite measure spaces" Publ. Math. Debrecen , 14 (1967) pp. 79–81 -finite measure spaces" Publ. Math. Debrecen , 14 (1967) pp. 79–81 |
| [8] | J.P. Conze, "Entropie d'un groupe abélien de transformations" Z. Wahrsch. Verw. Gebiete , 25 : 1 (1972) pp. 11–30 |
| [9] | R.M. Burton, "An asymptotic definition of 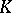 -groups of automorphisms" Z. Wahrsch. Verw. Gebiete , 47 : 2 (1979) pp. 207–212 -groups of automorphisms" Z. Wahrsch. Verw. Gebiete , 47 : 2 (1979) pp. 207–212 |
| [10] | S. Dani, "Kolmogorov automorphisms on homogeneous spaces" Amer. J. Math. , 98 : 1 (1976) pp. 119–163 |
| [11] | U. Krengel, L. Sucheston, "Note on shift-invariant sets" Ann. Math. Statist. , 40 : 2 (1969) pp. 694–696 |
| [12] | B. Kamiński, "A note on 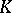 -systems" Bull. Acad. Polon. Sci. Sér. Sci. Math. Astr. Phys. , 26 : 2 (1978) pp. 95–97 -systems" Bull. Acad. Polon. Sci. Sér. Sci. Math. Astr. Phys. , 26 : 2 (1978) pp. 95–97 |
| [13] | Ya.G. Sinai, et al., "Dynamical systems" , 4 , Springer (1988) (Translated from Russian) |
| [14] | N.F.G. Martin, J.W. England, "Mathematical theory of entropy" , Addison-Wesley (1981) |
K-system(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=K-system(2)&oldid=18048