Jordan theorem
A plane simple closed curve  decomposes the plane
decomposes the plane  into two connected components and is their common boundary. Established by C. Jordan [1]. Together with the similar assertion: A simple arc does not decompose the plane, this is the oldest theorem in set-theoretic topology.
into two connected components and is their common boundary. Established by C. Jordan [1]. Together with the similar assertion: A simple arc does not decompose the plane, this is the oldest theorem in set-theoretic topology.
Of the two components, one (the inside of  ) is bounded; it is characterized by the fact that the order of every point in it with respect to
) is bounded; it is characterized by the fact that the order of every point in it with respect to  is
is  ; the other (the outside of
; the other (the outside of  ) is unbounded, and the orders of its points with respect to
) is unbounded, and the orders of its points with respect to  are zero. For any point
are zero. For any point  of the bounded component
of the bounded component  and every point
and every point 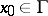 , there exists a simple arc with ends
, there exists a simple arc with ends 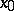 and
and  and all points of which, except
and all points of which, except 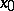 , are contained in
, are contained in 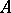 (Schoenflies' theorem).
(Schoenflies' theorem).
The Jordan (curve) theorem can be generalized according to the dimension: Every 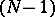 -dimensional submanifold of
-dimensional submanifold of 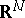 homeomorphic to a sphere decomposes the space into two components and is their common boundary; for
homeomorphic to a sphere decomposes the space into two components and is their common boundary; for 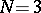 this was proved by e dimension','../l/l057830.htm','Lebesgue function','../l/l057840.htm','Lebesgue inequality','../l/l057850.htm','Lebesgue integral','../l/l057860.htm','Lebesgue measure','../l/l057870.htm','Lebesgue summation method','../l/l057940.htm','Lebesgue theorem','../l/l057950.htm','Measure','../m/m063240.htm','Metric space','../m/m063680.htm','Metric theory of functions','../m/m063700.htm','Orthogonal series','../o/o070370.htm','Perron method','../p/p072370.htm','Potential theory','../p/p074140.htm','Regular boundary point','../r/r080680.htm','Singular integral','../s/s085570.htm','Suslin theorem','../s/s091480.htm','Urysohn–Brouwer lemma','../u/u095860.htm','Vitali variation','../v/v096790.htm')" style="background-color:yellow;">H. Lebesgue, and in the general case by L.E.J. Brouwer, whence the
this was proved by e dimension','../l/l057830.htm','Lebesgue function','../l/l057840.htm','Lebesgue inequality','../l/l057850.htm','Lebesgue integral','../l/l057860.htm','Lebesgue measure','../l/l057870.htm','Lebesgue summation method','../l/l057940.htm','Lebesgue theorem','../l/l057950.htm','Measure','../m/m063240.htm','Metric space','../m/m063680.htm','Metric theory of functions','../m/m063700.htm','Orthogonal series','../o/o070370.htm','Perron method','../p/p072370.htm','Potential theory','../p/p074140.htm','Regular boundary point','../r/r080680.htm','Singular integral','../s/s085570.htm','Suslin theorem','../s/s091480.htm','Urysohn–Brouwer lemma','../u/u095860.htm','Vitali variation','../v/v096790.htm')" style="background-color:yellow;">H. Lebesgue, and in the general case by L.E.J. Brouwer, whence the 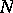 -dimensional theorem is sometimes called the Jordan–Brouwer theorem or Jordan–Brouwer separation theorem.
-dimensional theorem is sometimes called the Jordan–Brouwer theorem or Jordan–Brouwer separation theorem.
References
| [1] | C. Jordan, "Cours d'analyse" , 1 , Gauthier-Villars (1893) |
| [2] | Ch.J. de la Valleé-Poussin, "Cours d'analyse infinitésimales" , 2 , Libraire Univ. Louvain (1925) |
| [3] | P.S. Aleksandrov, "Combinatorial topology" , Graylock , Rochester (1956) (Translated from Russian) |
| [4] | J.A. Dieudonné, "Foundations of modern analysis" , Acad. Press (1961) (Translated from French) |
| [5] | W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948) |
| [6] | A.F. Filippov, "An elementary proof of Jordan's theorem" Uspekhi Mat. Nauk , 5 : 5 (1950) pp. 173–176 (In Russian) |
Comments
Jordan's theorem in 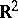 (or
(or  ) is often called the Jordan curve theorem; it was first proved rigorously by O. Veblen [a4].
) is often called the Jordan curve theorem; it was first proved rigorously by O. Veblen [a4].
C. Kuratowski strengthened Schoenflies' theorem by showing that there is in fact a homeomorphism from the closed unit disc that maps the boundary 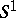 onto
onto 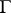 and the interior onto the inside of
and the interior onto the inside of 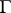 ; the Riemann mapping theorem (cf. Riemann theorem) then actually gives a homeomorphism that is analytic in the interior.
; the Riemann mapping theorem (cf. Riemann theorem) then actually gives a homeomorphism that is analytic in the interior.
The analogue of this strengthening is false in higher dimensions, as is shown by the famous "horned sphere of Alexanderhorned sphere" of J.W. Alexander (see [a1]).
References
| [a1] | R.H. Bing, "The geometric topology of  -manifolds" , Amer. Math. Soc. (1983) -manifolds" , Amer. Math. Soc. (1983) |
| [a2] | J. Dugundji, "Topology" , Allyn & Bacon (1966) (Theorem 8.4) |
| [a3] | J. van Mill, "Infinite-dimensional topology, prerequisites and introduction" , North-Holland (1988) |
| [a4] | O.Veblen, "Theory of plane curves in non-metrical Analysis Situs" Trans. Amer. Math. Soc. , 6 (1905) pp. 83–98 |
Jordan theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jordan_theorem&oldid=16776