Jordan algebra
An algebra in which the identities
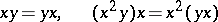 |
hold. Such algebras first arose in the paper [1] of P. Jordan devoted to the axiomatic foundation of quantum mechanics (cf. also [2]), and later found application in algebra, analysis and geometry.
Let 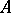 be an associative algebra over a field of characteristic
be an associative algebra over a field of characteristic 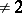 (cf. also Associative rings and algebras). The set
(cf. also Associative rings and algebras). The set 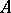 together with the operations of addition and Jordan multiplication
together with the operations of addition and Jordan multiplication
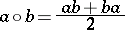 |
forms the algebra  , which is a Jordan algebra. A Jordan algebra that is isomorphic to a subalgebra of
, which is a Jordan algebra. A Jordan algebra that is isomorphic to a subalgebra of 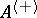 for some associative algebra
for some associative algebra 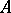 is called special. The role of special algebras in the theory of Jordan algebras is in many respects analogous to the role of associative algebras in the theory of alternative algebras (cf. also Alternative rings and algebras). At the basis of this analogy lies the theorem that every two-generated subalgebra of a Jordan algebra is special. (Every two-generated subalgebra of an alternative algebra is associative.) However, the class of special Jordan algebras is not a variety, i.e. it is not given by identities, since special Jordan algebras can have non-special homomorphic images. Nevertheless, identities of degree 8 or 9 have been found that are satisfied by every special Jordan algebra, but are not satisfied by some non-special algebra, while it has been proved that such identities of degree
is called special. The role of special algebras in the theory of Jordan algebras is in many respects analogous to the role of associative algebras in the theory of alternative algebras (cf. also Alternative rings and algebras). At the basis of this analogy lies the theorem that every two-generated subalgebra of a Jordan algebra is special. (Every two-generated subalgebra of an alternative algebra is associative.) However, the class of special Jordan algebras is not a variety, i.e. it is not given by identities, since special Jordan algebras can have non-special homomorphic images. Nevertheless, identities of degree 8 or 9 have been found that are satisfied by every special Jordan algebra, but are not satisfied by some non-special algebra, while it has been proved that such identities of degree 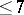 do not exist. A necessary and sufficient condition on an algebra to be special is: A Jordan algebra is special if and only if it can be isomorphically imbedded in a Jordan algebra each countable subset of which lies in a subalgebra generated by two elements.
do not exist. A necessary and sufficient condition on an algebra to be special is: A Jordan algebra is special if and only if it can be isomorphically imbedded in a Jordan algebra each countable subset of which lies in a subalgebra generated by two elements.
Examples.
1) Let 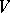 be a vector space over a field with a symmetric bilinear form
be a vector space over a field with a symmetric bilinear form  , and let
, and let 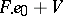 be a space of one dimension higher, on which
be a space of one dimension higher, on which
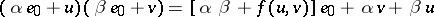 |
determines the multiplication (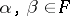 ;
; 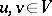 ). The algebra that arises is called the algebra with symmetric bilinear form
). The algebra that arises is called the algebra with symmetric bilinear form 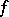 . It can be isomorphically imbedded in the algebra
. It can be isomorphically imbedded in the algebra 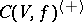 , where
, where 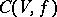 is the Clifford algebra of
is the Clifford algebra of 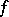 , and is therefore a special Jordan algebra.
, and is therefore a special Jordan algebra.
2) Let 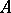 be an associative algebra and
be an associative algebra and 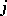 an involution of it (an anti-isomorphism of order two). The set
an involution of it (an anti-isomorphism of order two). The set
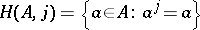 |
is a subalgebra in 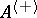 and is also a special Jordan algebra.
and is also a special Jordan algebra.
3) Let 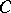 be an alternative non-associative algebra over a field
be an alternative non-associative algebra over a field 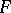 with involution
with involution 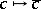 whose fixed elements lie in the associative centre of
whose fixed elements lie in the associative centre of 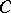 . In the algebra
. In the algebra  of matrices over
of matrices over 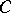 of order 3, the set
of order 3, the set
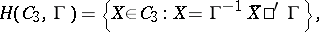 |
where
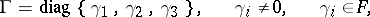 |
is a non-special Jordan algebra under the operations of addition and Jordan multiplication. This algebra is not the homomorphic image of any special algebra.
The finite-dimensional simple Jordan algebras over an algebraically closed field 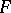 of characteristic
of characteristic 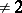 have been completely classified (cf. [3]). The central simple finite-dimensional Jordan algebras split into five series. The series –(D) are infinite and consist of special algebras, (E) consists of a single non-special algebra:
have been completely classified (cf. [3]). The central simple finite-dimensional Jordan algebras split into five series. The series –(D) are infinite and consist of special algebras, (E) consists of a single non-special algebra:
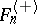 ;
;
(B) 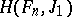 , where
, where  ;
;
(C) 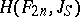 , where
, where 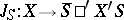 ,
, 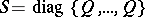 ,
,
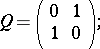 |
(D) 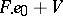 — the algebras of symmetric non-degenerate bilinear forms;
— the algebras of symmetric non-degenerate bilinear forms;
(E) 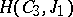 , where
, where 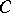 is the Cayley–Dickson algebra with the standard involution. This algebra is
is the Cayley–Dickson algebra with the standard involution. This algebra is  -dimensional over
-dimensional over 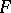 .
.
In each finite-dimensional Jordan algebra 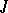 the radical (the largest nil radical)
the radical (the largest nil radical) 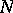 is involutory and the quotient algebra
is involutory and the quotient algebra 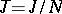 is a finite direct sum of simple Jordan algebras. If
is a finite direct sum of simple Jordan algebras. If 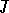 is separable, then
is separable, then 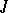 has a decomposition
has a decomposition 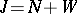 into the sum of the radical and a semi-simple subalgebra
into the sum of the radical and a semi-simple subalgebra 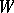 that is isomorphic to
that is isomorphic to 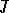 . In the case of characteristic 0, all semi-simple terms
. In the case of characteristic 0, all semi-simple terms 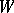 are conjugate relative to automorphisms of a special kind (cf. [3]). This is also true in characteristic
are conjugate relative to automorphisms of a special kind (cf. [3]). This is also true in characteristic 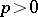 if some restrictions are imposed on the algebra.
if some restrictions are imposed on the algebra.
A generalization of the theory of finite-dimensional Jordan algebras is the theory of Jordan algebras with the minimum condition for quadratic (inner) ideals (cf. [3], [4], [5]). A quadratic ideal 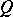 of an algebra
of an algebra 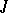 is a subspace for which
is a subspace for which 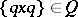 for all
for all 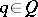 and
and 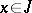 , where
, where 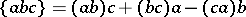 is the triple Jordan product. If
is the triple Jordan product. If 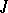 is a Jordan algebra with the minimum condition for quadratic ideals and
is a Jordan algebra with the minimum condition for quadratic ideals and 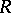 is its quadratic radical (cf. Radical of rings and algebras), then the quotient algebra
is its quadratic radical (cf. Radical of rings and algebras), then the quotient algebra 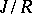 is a finite direct sum of simple algebras, which have been described apart from the Jordan algebras with division. If
is a finite direct sum of simple algebras, which have been described apart from the Jordan algebras with division. If 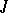 is a special algebra, it has been proved that the radical
is a special algebra, it has been proved that the radical  is nilpotent and finite-dimensional.
is nilpotent and finite-dimensional.
An algebraic special Jordan algebra (cf. also Algebraic algebra) that satisfies a non-trivial (for special algebras) identity is locally finite-dimensional; a special Jordan nil algebra (cf. also Nil algebra) with a non-trivial identity is locally nilpotent [6]. In particular, a special algebraic Jordan (nil) algebra of bounded index is locally finite-dimensional (nilpotent). A finitely-generated solvable Jordan algebra is nilpotent; this is not true for special algebras in the general case. A Jordan 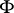 -operator ring that is a finitely-generated
-operator ring that is a finitely-generated 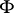 -module with nilpotent generating elements, is nilpotent [7].
-module with nilpotent generating elements, is nilpotent [7].
With each Jordan algebra one can in various ways associate a Lie algebra (cf. [3], [8]). A number of theorems on Jordan algebras have been obtained from known theorems on Lie algebras. E.g., it has been proved that a semi-simple finite-dimensional Jordan algebra over an algebraically closed field of characteristic zero has a basis with integral structure constants. For the theory of Lie algebras this construction is also useful, since certain important classes of Lie algebras can be realized by it. E.g., the Lie algebra of derivations of the simple Lie algebra of type (E) is the exceptional simple Lie algebra 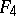 , the algebra of linear transformations of this algebra that leave invariant some cubic form is the exceptional simple Lie algebra
, the algebra of linear transformations of this algebra that leave invariant some cubic form is the exceptional simple Lie algebra 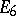 . All five exceptional Lie algebras of types
. All five exceptional Lie algebras of types 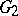 ,
,  ,
, 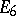 ,
,  ,
, 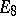 can be realized by another construction, associating to an alternative algebra of degree 2 and a Jordan algebra of degree 3 some Lie algebra.
can be realized by another construction, associating to an alternative algebra of degree 2 and a Jordan algebra of degree 3 some Lie algebra.
It is, finally, interesting to note that some algebras arising in genetics are Jordan algebras [10].
References
| [1] | P. Jordan, "Ueber Verallgemeinerungsmöglichkeiten des Formalismus der Quantenmechanik" Nachr. Akad. Wiss. Göttingen. Math. Phys. Kl. I , 41 (1933) pp. 209–217 |
| [2] | G.G. Emch, "Algebraic methods in statistical mechanics and quantum field theory" , Wiley (1972) |
| [3] | N. Jacobson, "Structure and representations of Jordan algebras" , Amer. Math. Soc. (1968) |
| [4] | K. McCrimmon, "The radical of a Jordan algebra" Proc. Nat. Acad. Sci. USA , 62 : 3 (1969) pp. 671–678 |
| [5] | A.M. Slin'ko, "On the Jacobson radical and absolute zero divisors of special Jordan algebras" Algebra and Logic , 11 : 6 (1972) pp. 396–402 Algebra i Logika , 11 : 6 (1972) pp. 711–724 |
| [6] | A.I. Shirshov, "On some non-associative null rings and algebraic algebras" Mat. Sb. , 41 : 3 (1957) pp. 381–394 (In Russian) |
| [7] | I.P. Shestakov, "Certain classes of noncommutative Jordan rings" Algebra and Logic , 10 : 4 (1971) pp. 252–280 Algebra i Logika , 10 : 4 (1971) pp. 407–448 |
| [8] | R.D. Schafer, "An introduction to nonassociative algebras" , Acad. Press (1966) |
| [9] | S.R. Gordon, "An integral basis theorem for Jordan algebras" J. of Algebra , 24 (1973) pp. 258–282 |
| [10] | R.D. Schafer, "Structure of genetic algebras" Amer. J. Math. , 71 (1949) pp. 121–135 |
| [11] | M. Koecher, "An elementary approach to bounded symmetric domains" , Rice Univ. (1969) |
| [12] | A.M. Slin'ko, et al., "Jordan algebras" , 1 , Novosibirsk (1976) (In Russian) |
Comments
For Jordan algebras in genetics see also Genetic algebra.
There exists a functor Kan [a1], called the Kantor functor, which establishes an isomorphism between the category of Jordan algebras and the category of 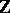 -graded Lie algebras of the form
-graded Lie algebras of the form  with the following properties [a2]:
with the following properties [a2]:
a) if 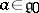 or
or 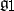 and
and 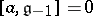 , then
, then 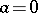 ;
;
b) 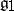 contains an element
contains an element 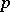 such that
such that 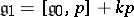 , and
, and  generates the subalgebra
generates the subalgebra 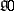 (
(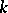 is the base field).
is the base field).
The construction of 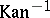 is very simple:
is very simple: 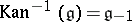 with product
with product 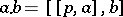 .
.
This construction was extended to the super-algebra case and used to classify simple finite-dimensional Jordan super-algebras [a2].
References
| [a1] | I.L. Kantor, "Classification of irreducible transitively differential groups" Soviet Math. Dokl. , 5 (1964) pp. 1404–1407 Dokl. Akad. Nauk SSSR , 158 : 5 (1964) pp. 1271–1274 |
| [a2] | V.G. Kac, "Classification of simple 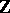 -graded Lie superalgebras and simple Jordan superalgebras" Comm. in Algebra , 5 : 13 (1977) pp. 1375–1400 -graded Lie superalgebras and simple Jordan superalgebras" Comm. in Algebra , 5 : 13 (1977) pp. 1375–1400 |
| [a3] | H. Braun, M. Koecher, "Jordan-algebren" , Springer (1966) |
| [a4] | T.A. Springer, "Jordan algebras and algebraic groups" , Springer (1973) |
Jordan algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jordan_algebra&oldid=16524