Jacobi polynomials

Orthogonal polynomials on the interval 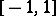with the weight function

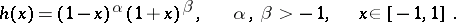The standardized Jacobi polynomials are defined by the Rodrigues formula:

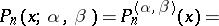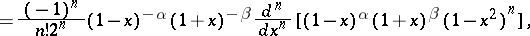and the orthonormal Jacobi polynomials have the form

The polynomial 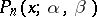satisfies the differential equation

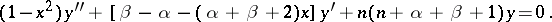When and , the orthonormal Jacobi polynomials satisfy the following weighted estimate:

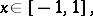where the constant 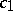does not depend on and . At 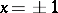the sequence grows at a rate and 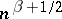, respectively.

Fourier series in Jacobi polynomials (cf. Fourier series in orthogonal polynomials) inside the interval 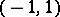are similar to trigonometric Fourier series. But in neighbourhoods of the end points of this interval, the orthogonality properties of Fourier–Jacobi series are different, because at 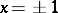the orthonormal Jacobi polynomials grow unboundedly. The Fourier–Jacobi series of a function 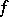is uniformly convergent on 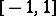if is 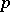times continuously differentiable on this segment and 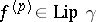with , where

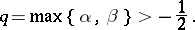Under these conditions the following inequality holds:

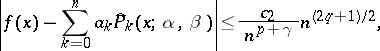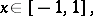where the constant 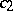does not depend on and . On the other hand, when and 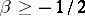, the remainder in the Fourier–Jacobi series for satisfies the following weighted estimate:

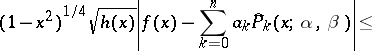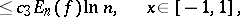where 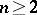, the constant 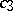does not depend on and , and 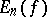is the best uniform approximation error (cf. Best approximation) of the continuous functi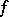on on 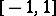by polynomials of degree not exceeding .

The Jacobi polynomials were introduced by C.G.J. Jacobi [1] in connection with the solution of the hypergeometric equation. Special cases of the Jacobi polynomials are: the Legendre polynomials (when 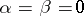); the Chebyshev polynomials of the first kind (when ); the Chebyshev polynomials of the second kind (when 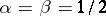); and the ultraspherical polynomials (when ).

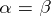See also Classical orthogonal polynomials.

References

[1]	C.G.J. Jacobi, "Untersuchungen über die Differentialgleichung der hypergeometrischen Reihe" J. Reine Angew. Math. , 56 (1859) pp. 149–165
[2]	P.K. Suetin, "Classical orthogonal polynomials" , Moscow (1978) (In Russian)

Comments

See also [a4], [a1] and Fourier series in orthogonal polynomials.

Let 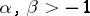and 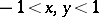. Then there is a product formula of the form

with positive measure 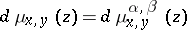if and only if 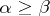and either or 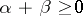. This yields a positive convolution structure for Jacobi series. For 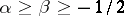the above measure can be computed explicitly from the addition formula for Jacobi polynomials. See [a1], Lecture 4.

For the dual problem one has

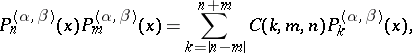with 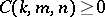if 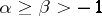, 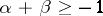. This yields a positive dual convolution structure for Jacobi series. See [a1], Lecture 5.

Jacobi polynomials admit many different group-theoretic interpretations. The three most important ones are as matrix elements of the irreducible representations of 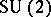(cf. [a5], Chapt. 3), as -invariant spherical harmonics on the unit sphere in 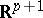(cf. [a2]) and as zonal spherical functions on the compact symmetric spaces of rank one (cf. [a3], Chapt. 5, §4.3).

References

[a1]	R. Askey, "Orthogonal polynomials and special functions" , Reg. Conf. Ser. Appl. Math. , 21 , SIAM (1975)
[a2]	B.L.J. Braaksma, B. Meulenbeld, "Jacobi polynomials as spherical harmonics" Nederl. Akad. Wetensch. Proc. Ser. A , 71 (1968) pp. 384–389
[a3]	S. Helgason, "Groups and geometric analysis" , Acad. Press (1984) pp. Chapt. II, Sect. 4
[a4]	G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975)
[a5]	N.Ya. Vilenkin, "Special functions and the theory of group representations" , Amer. Math. Soc. (1968) (Translated from Russian)