Difference between revisions of "Ising model"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 141 formulas out of 142 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 142 formulas, 141 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A model [[#References|[a1]]] defined by the following Hamiltonian (cf. [[Hamilton function|Hamilton function]]) $\mathcal{H}$ (i.e. energy functional of variables; in this case the "spins" $S _ { i } = \pm 1$ on the $N$ sites of a regular lattice in a space of dimension $d$) | ||
| − | + | \begin{equation} \tag{a1} \mathcal{H} = - \sum _ { i < j = 1 } ^ { N } J _ { i j } S _ { i } S _ { j } - H \sum _ { i = 1 } ^ { N } S _ { i }. \end{equation} | |
| − | + | Here, $J _ {i j }$ are "exchange constants" , $H$ is a (normalized) magnetic field, involving an interpretation of the model to describe magnetic ordering in solids ($M = \sum _ { i = 1 } ^ { N } S _ { i }$ is "magnetization" , the Zeeman energy $- H M$ in (a1) is the energy gained due to application of the field). | |
| − | + | Since its solution for $d = 1$ in 1925 [[#References|[a1]]], the model became a "fruitfly" for the development of both concepts and techniques in statistical thermodynamics. It appears also in other interpretations in lattice statistics: defining occupation variables $\rho _ { i } = ( 1 - S _ { i } ) / 2$, where lattice site $i$ is empty ($\rho _ { i } = 0$) if $S _ { i } = 1$ or occupied ($\rho _ { i } = 1$) if $S _ { i } = - 1$. This is the lattice gas model of a fluid. One can also interpret the cases $S _ { i } = \pm 1$ as two chemical species $A$, $B$ for describing ordering or unmixing of binary alloys $( A B )$, etc. | |
| − | + | Statistical thermodynamics [[#References|[a2]]] aims to compute average properties of systems with a large number of degrees of freedom (i.e., in the thermodynamic limit $N = \infty$). These averages at a temperature $T$ are obtained from the free energy $F ( T , H )$ (per spin) or the partition function $Z$, | |
| − | + | \begin{equation} \tag{a2} F = - \frac { k _ { B } T \operatorname { ln } Z } { N } , \quad Z = \operatorname { Tr } \operatorname { exp } \left( - \frac { \mathcal{H} } { k _ { B } T } \right). \end{equation} | |
| − | + | Here, $k _ { B }$ is the Boltzmann constant [[#References|[a2]]], and the trace operation $\operatorname { Tr}$ stands for a sum over all the states in the phase space of the system (which here is the set of $2 ^ { N }$ states $S _ { 1 } = \pm 1 , \dots , S _ { N } = \pm 1$). Magnetization per spin $m \equiv \langle M \rangle _ { T } / N$, susceptibility <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i120/i120080/i12008031.png"/>, entropy $S$, etc. are then found as partial derivatives of $F$ [[#References|[a2]]]: | |
| − | + | \begin{equation} \tag{a3} \left\{ \begin{array}{l}{ m = - \left( \frac { \partial F } { \partial H } \right) _ { T }, }\\{ \chi = \left( \frac { \partial m } { \partial H } \right) _ { T }, }\\{ S = - \left( \frac { \partial F } { \partial T } \right) _ { H }, }\end{array} \right. \end{equation} | |
| − | + | where $\langle A \rangle _ { T }$ stands for a canonical average of a quantity $A$: | |
| − | + | \begin{equation*} \langle A \rangle _ { T } = Z ^ { - 1 } \operatorname { Tr } \left[ \operatorname { exp } ( - \frac { \mathcal{H} } { k _ { B } T } ) A \right]. \end{equation*} | |
| − | + | The Ising model is important since for $d \geq 2$ it exhibits phase transitions. In the simplest case, $J _ { i j } = J$ if sites $i$, $j$ are nearest neighbours on the lattice and zero elsewhere, a transition occurs for $J > 0$ from a paramagnet ($T > T _ { c }$) to a ferromagnet ($T < T _ { c }$) at a critical temperature $T _ { c }$. In the disordered paramagnet $\operatorname { lim } _ { H \rightarrow 0 } m ( T , H ) = 0$, while in the ordered ferromagnet the spontaneous magnetization $m_S$ occurs: | |
| − | + | \begin{equation} \tag{a4} m _ { s } = \operatorname { lim } _ { H \rightarrow 0 } m ( T , H ) > 0. \end{equation} | |
| − | + | This is an example of spontaneous symmetry breaking: $\mathcal{H}$ for $H = 0$ does not single out a sign of $m$ (replacing all $\{ S _ { i } \}$ by $\{ - S _ { i } \}$ leaves $\mathcal{H}$ invariant). However, for $T < T _ { c }$ and $H = 0$ the equilibrium state of the system is two-fold degenerate ($\pm m _ { s }$). This degeneracy is already obvious from the groundstate of (a1), for $T \rightarrow 0$, found from the absolute minimum of $H$ as a functional of the $\{ S _ { i } \}$: for $H = 0$ this minimum occurs for either all $S _ { i } = + 1$ or all $S _ { i } = - 1$. | |
| − | + | Interestingly, for $d = 1$ no such phase transition at $T _ { c } > 0$ occurs; rather $T _ { c } = 0$ [[#References|[a1]]]. The problem (a1)–(a3) is solved exactly by transfer matrix methods [[#References|[a3]]]. Rewriting (a1) as $H = - J \sum _ { i = 1 } ^ { N } S _ { i } S _ { i+ 1 } - {\cal H} \sum _ { i = 1 } ^ { N } S _ { i }$ with the periodic boundary condition $S _ { N + 1 } = S _ { 1 }$, one finds | |
| − | + | \begin{equation} \tag{a5} Z = \sum _ { S _ { 1 } = \pm 1 } \ldots \sum _ { S _ { N } = \pm 1 } \end{equation} | |
| − | + | \begin{equation*} \operatorname { exp } \left\{ \frac { 1 } { k _ { B } T } \sum _ { i = 1 } ^ { N } [ J S _ { i } S _ { i+ 1 } + \frac { H } { 2 } ( S _ { i } + S _ { i+ 1 } ) ] \right\} = \end{equation*} | |
| − | + | \begin{equation*} = \sum _ { S _ { 1 } = \pm 1 } \cdots \sum _ { S _ { N } = \pm 1 } \prod _ { i = 1 } ^ { N } \end{equation*} | |
| − | + | \begin{equation*} \operatorname { exp } \left\{ \frac { 1 } { k _ { B } T } \left[ J S _ { i } S _ { i + 1 } + \frac { H } { 2 } ( S _ { i } + S _ { i + 1 } ) \right] \right\} = \end{equation*} | |
| − | + | \begin{equation*} = \sum _ { S _ { 1 } = \pm 1 } \ldots \sum _ { S _ { N } = \pm 1 } \prod _ { i = 1 } ^ { N } \langle S _ { i } | \mathcal{P} | S _ { i+ 1 } \rangle \end{equation*} | |
| − | + | The $( 2 \times 2 )$-matrix ${\cal P} = ( P _ { s s ^ { \prime } } ) = ( \langle S | {\cal P} | S ^ { \prime } \rangle )$ is defined as | |
| − | + | \begin{equation} \tag{a6} \mathcal{P} \equiv \left( \begin{array} { c c } { \operatorname { exp } \left( \frac { J + H } { k _ { B } T } \right) } & { \operatorname { exp } \left( \frac { - J } { k _ { B } T } \right) } \\ { \operatorname { exp } \left( \frac { - J } { k _ { B } T } \right) } & { \operatorname { exp } \left( \frac { J - H } { k _ { B } T } \right) } \end{array} \right). \end{equation} | |
| − | + | Now $Z$ is simply the trace of an $N$-fold matrix product, | |
| − | + | \begin{equation} \tag{a7} Z = \sum _ { S _ { 1 } = \pm 1 } \left( S _ { 1 } | \mathcal{P} ^ { N } | S _ { 1 } \right) = \lambda _ { + } ^ { N } + \lambda ^ { N }_{-}, \end{equation} | |
| − | where the | + | where the property was used that the trace of a symmetric matrix is independent of the representation, and so one can evaluate the trace by first diagonalizing $\mathcal{P}$, |
| − | + | \begin{equation} \tag{a8} \mathcal{P} = \left( \begin{array} { c c } { \lambda _ { + } } & { 0 } \\ { 0 } & { \lambda _ { - } } \end{array} \right) , \quad \mathcal{P} ^ { N } = \left( \begin{array} { c c } { \lambda _ { + } ^ { N } } & { 0 } \\ { 0 } & { \lambda ^ { N } } \end{array} \right), \end{equation} | |
| − | + | where the eigenvalues $\lambda _ { + }$, $\lambda_{-}$ are found from the vanishing of the determinant, $\operatorname { det } ( \mathcal{P} - \lambda \mathcal{I} ) = 0$, $\cal I$ being the unit $( 2 \times 2 )$-matrix: | |
| − | + | \begin{equation} \tag{a9} \lambda _ { \pm } = \operatorname { exp } \left( \frac { J } { k _ { B } T } \right) \operatorname { cosh } \left( \frac { H } { k _ { B } T } \right) \pm \end{equation} | |
| − | + | \begin{equation*} \pm \left[ \operatorname { exp } ( \frac { 2 J } { k _ { B } T } ) \operatorname { cosh } ^ { 2 } ( \frac { H } { k _ { B } T } ) - 2 \operatorname { sinh } ( \frac { 2 J } { k _ { B } T } ) \right] ^ { 1 / 2 }. \end{equation*} | |
| − | + | In the limit $N \rightarrow \infty$ the largest eigenvalue dominates, $Z \rightarrow \lambda _ { + } ^ { N } $, and hence | |
| − | + | \begin{equation} \tag{a10} F = - k _ { B } T \operatorname { ln } \lambda _ { + } = \end{equation} | |
| − | + | \begin{equation*} = - J - k _ { B }T \operatorname { ln } \left\{ \operatorname { cosh } \left( \frac { H } { k _ { B } T } \right) + + \left[ \operatorname { sinh } ^ { 2 } \left( \frac { H } { k _ { B } T } \right) + \operatorname { exp } \left( - \frac { 4 J } { k _ { B } T } \right) \right] ^ { 1 / 2 } \right\}, \end{equation*} | |
| − | + | \begin{equation} \tag{a11} m = \frac { \operatorname { sinh } \left( \frac { H } { k _ { B } T } \right) } { [ \operatorname { sinh } ^ { 2 } \left( \frac { H } { k _ { B } T } \right) + \operatorname { exp } \left( - \frac { 4 J } { k _ { B } T } \right) ] ^ { 1 / 2 } }. \end{equation} | |
| − | + | Indeed, for $T > 0$ there is no spontaneous magnetization, and for $H \rightarrow 0$ the susceptibility becomes $\chi = ( k _ { B } T ) ^ { - 1 } \operatorname { exp } ( 2 J / k _ { B } T )$. | |
| − | + | It is remarkable that (a11) strongly contradicts the popular molecular field approximation (MFA). In the molecular field approximation one replaces in the interaction of every spin $S _ { i }$ with its neighbours, $[ S _ { i } ( S _ { i - 1 } + S _ { i + 1 } ) ]$, the spins by their averages, $S _ { i - 1 } \rightarrow \langle m \rangle$; $S_{i + 1 }\rightarrow \langle m \rangle$, the problem becomes a single-site Hamiltonian where $S _ { i }$ is exposed to an effective field $H _ { \text{eff} } = H + 2 m J$, which needs to be calculated self-consistently; carrying out the average over the two states $S _ { i } = \pm 1$ one finds | |
| − | + | \begin{equation} \tag{a12} m = \frac { \operatorname { exp } \Bigl( \frac { H _ { \text{eff} } } { k _ { B } T }\Bigr ) - \operatorname { exp } \Bigl( - \frac { H _ {\text{eff} } } { k _ { B } T }\Bigr ) } { \operatorname { exp }\Bigl ( \frac { H _ { \text{eff} } } { k _ { B } T }\Bigr ) + \operatorname { exp } \Bigl( - \frac { H _ { \text{eff} } } { k _ { B } T } \Bigr) } = \end{equation} | |
| − | + | \begin{equation*} = \operatorname { tanh } [ \frac { H + 2 m J } { k _ { B } T } ], \end{equation*} | |
| − | + | which yields $T _ { c } = 2 J / k _ { B }$ and $m _ { s } \propto ( 1 - T / T _ { c } ) ^ { \beta }$ with a critical exponent $\beta = 1 / 2$, and a Curie–Weiss law for $\chi ( \chi \propto ( T / T _ { c } - 1 ) ^ { - \gamma } \text { with } \gamma = 1 )$. Thus, the Ising model shows that the molecular field approximation in this case yields unreliable and misleading results! | |
| − | Another extension adds "time t" as a variable: by a transition probability | + | For the Ising-model in $d = 2$, exact transfer matrix methods are applicable for $H = 0$; they show that a phase transition at $T _ { c } > 0$ does exist [[#References|[a3]]], [[#References|[a4]]], [[#References|[a5]]]. But the critical exponents $\beta$, $\gamma$ differ very much from their molecular field approximation values; namely, $\beta = 1 / 8$ and $\gamma = 7 / 4$. This is important, since the exponents $\beta = 1 / 2$ and $\gamma = 1$ also follow from the Landau theory of phase transitions [[#References|[a2]]], which only requires that $F$ can be expanded in a power series in $m$, with the coefficient at the $m ^ { 2 }$ term changing sign at $T _ { c }$ as $T / T _ { c } \rightarrow 1$, which are plausible assumptions on many grounds. The $d = 2$ Ising model testifies that neither molecular field approximation nor Landau theory are correct. The Ising model then prompted the development of entirely new theoretical concepts, namely [[Renormalization group analysis|renormalization group analysis]] [[#References|[a6]]], by which one can understand how non-mean-field critical behaviour arises. The Ising model also became a very useful testing ground for many numerical methods: e.g. systematic expansions of $F$ at low $T$ (in the variable $u = \operatorname { exp } ( - 4 J / k _ { B } T )$) or at high $T$ in the variable $v = \operatorname { tanh } ( J / k _ { B } T )$ [[#References|[a7]]], or Monte-Carlo methods [[#References|[a8]]]. It also played a pivotal role for the concepts on surface effects on phase transitions, and for phase coexistence (domains of oppositely oriented magnetization, separated by walls). Such problems were described with a mathematical rigor that is seldomly found in the statistical thermodynamics of many-body systems. Rigorous work includes the existence of a spontaneous magnetization for $d \geq 2$ ( "Peierls proof" ), inequalities between spin correlations, theorems on the zeros of the partition function, etc.; see [[#References|[a9]]]. The Ising model is the yardstick against which each new approach is measured. |
| + | |||
| + | Finally, there are extensions of the Ising model. One direction is to make the $J _ {i j }$ more complicated rather than uniformly ferromagnetic ($J _ { i j } > 0$). E.g., if in one lattice direction $J _ { 1 } > 0$ between nearest neighbours but $J _ { 2 } < 0$ between next nearest neighbours, the resulting anisotropic next nearest neighbour Ising model (ANNNI model) is famous [[#References|[a10]]] for its phase diagram with infinitely many phases and transitions; choosing the $J _ { i j } = \pm J$ at random from a prescribed distribution, the resulting Ising spin glass [[#References|[a11]]] is a prototype model of glasses and other disordered solids. | ||
| + | |||
| + | Another extension adds "time t" as a variable: by a transition probability $w ( \{ S _ { i } \} \rightarrow \{ S _ { i } ^ { \prime } \} )$ per unit time one is led to a master equation for the probability that a state $\{ S _ { 1 } , \ldots , S _ { N } \}$ occurs at time $t$. Such kinetic Ising models [[#References|[a12]]] are most valuable to test concepts of non-equilibrium statistical mechanics, and provide the basis for simulations of unmixing in alloys ( "spinodal decomposition" ), etc. Finally, one can generalize the Ising model by replacing the spin $S _ { i } = \pm 1$ by a more complex variable, e.g. in the Potts model [[#References|[a13]]] each site may be in one of $p$ states where $p$ is integer (also, the limit $p \rightarrow 1$ is of interest; the so-called "percolation problem" [[#References|[a14]]]). The techniques for the Ising model (transfer matrix, series expansions, renormalization, Monte Carlo, etc.) are valuable for all these related problems, too. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> E. Ising, "Beitrag zur Theorie des Ferromagnetismus" ''Z. Phys.'' , '''31''' (1925) pp. 253–258</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> L.D. Landau, E.M. Lifshitz, "Statistical physics" , Pergamon (1958)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> R.J. Baxter, "Exactly solved models in statistical mechanics" , Acad. Press (1982)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> L. Onsager, "Crystal statistics I. A two-dimensional model with an order-disorder transition" ''Phys. Rev.'' , '''65''' (1944) pp. 117–149</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> B.M. McCoy, T.T. Wu, "The two-dimensional Ising model" , Harvard Univ. Press (1973)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> M.E. Fisher, "The renormalization group in the theory of critical behavior" ''Rev. Mod. Phys.'' , '''46''' (1974) pp. 597–616</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> "Phase Transitions and Critical Phenomena" C. Domb (ed.) M.S. Green (ed.) , '''3''' , Acad. Press (1974)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> "Monte Carlo methods in statistical physics" K. Binder (ed.) , Springer (1979)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> R.B. Griffiths, "Rigorous results and theorems" C. Domb (ed.) M.S. Green (ed.) , ''Phase Transitions and Critical Phenomena'' , '''1''' , Acad. Press (1972) pp. 7–109</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> W. Selke, "The Annni model-theoretical analysis and experimental application" ''Phys. Rep.'' , '''170''' (1988) pp. 213–264</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> K. Binder, A.P. Young, "Spin glasses: experimental facts, theoretical concepts, and open questions" ''Rev. Mod. Phys.'' , '''58''' (1986) pp. 801–976</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> K. Kawasaki, "Kinetics of Ising models" C. Domb (ed.) M.S. Green (ed.) , ''Phase Transitions and Critical Phenomena'' , '''2''' , Acad. Press (1972) pp. 443–501</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> F.Y. Wu, "The Potts model" ''Rev. Mod. Phys.'' , '''54''' (1982) pp. 235–268</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> D. Stauffer, A. Aharony, "Introduction to percolation theory" , Taylor&Francis (1992)</td></tr></table> |
Revision as of 16:55, 1 July 2020
A model [a1] defined by the following Hamiltonian (cf. Hamilton function) $\mathcal{H}$ (i.e. energy functional of variables; in this case the "spins" $S _ { i } = \pm 1$ on the $N$ sites of a regular lattice in a space of dimension $d$)
\begin{equation} \tag{a1} \mathcal{H} = - \sum _ { i < j = 1 } ^ { N } J _ { i j } S _ { i } S _ { j } - H \sum _ { i = 1 } ^ { N } S _ { i }. \end{equation}
Here, $J _ {i j }$ are "exchange constants" , $H$ is a (normalized) magnetic field, involving an interpretation of the model to describe magnetic ordering in solids ($M = \sum _ { i = 1 } ^ { N } S _ { i }$ is "magnetization" , the Zeeman energy $- H M$ in (a1) is the energy gained due to application of the field).
Since its solution for $d = 1$ in 1925 [a1], the model became a "fruitfly" for the development of both concepts and techniques in statistical thermodynamics. It appears also in other interpretations in lattice statistics: defining occupation variables $\rho _ { i } = ( 1 - S _ { i } ) / 2$, where lattice site $i$ is empty ($\rho _ { i } = 0$) if $S _ { i } = 1$ or occupied ($\rho _ { i } = 1$) if $S _ { i } = - 1$. This is the lattice gas model of a fluid. One can also interpret the cases $S _ { i } = \pm 1$ as two chemical species $A$, $B$ for describing ordering or unmixing of binary alloys $( A B )$, etc.
Statistical thermodynamics [a2] aims to compute average properties of systems with a large number of degrees of freedom (i.e., in the thermodynamic limit $N = \infty$). These averages at a temperature $T$ are obtained from the free energy $F ( T , H )$ (per spin) or the partition function $Z$,
\begin{equation} \tag{a2} F = - \frac { k _ { B } T \operatorname { ln } Z } { N } , \quad Z = \operatorname { Tr } \operatorname { exp } \left( - \frac { \mathcal{H} } { k _ { B } T } \right). \end{equation}
Here, $k _ { B }$ is the Boltzmann constant [a2], and the trace operation $\operatorname { Tr}$ stands for a sum over all the states in the phase space of the system (which here is the set of $2 ^ { N }$ states $S _ { 1 } = \pm 1 , \dots , S _ { N } = \pm 1$). Magnetization per spin $m \equiv \langle M \rangle _ { T } / N$, susceptibility 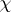 , entropy $S$, etc. are then found as partial derivatives of $F$ [a2]:
, entropy $S$, etc. are then found as partial derivatives of $F$ [a2]:
\begin{equation} \tag{a3} \left\{ \begin{array}{l}{ m = - \left( \frac { \partial F } { \partial H } \right) _ { T }, }\\{ \chi = \left( \frac { \partial m } { \partial H } \right) _ { T }, }\\{ S = - \left( \frac { \partial F } { \partial T } \right) _ { H }, }\end{array} \right. \end{equation}
where $\langle A \rangle _ { T }$ stands for a canonical average of a quantity $A$:
\begin{equation*} \langle A \rangle _ { T } = Z ^ { - 1 } \operatorname { Tr } \left[ \operatorname { exp } ( - \frac { \mathcal{H} } { k _ { B } T } ) A \right]. \end{equation*}
The Ising model is important since for $d \geq 2$ it exhibits phase transitions. In the simplest case, $J _ { i j } = J$ if sites $i$, $j$ are nearest neighbours on the lattice and zero elsewhere, a transition occurs for $J > 0$ from a paramagnet ($T > T _ { c }$) to a ferromagnet ($T < T _ { c }$) at a critical temperature $T _ { c }$. In the disordered paramagnet $\operatorname { lim } _ { H \rightarrow 0 } m ( T , H ) = 0$, while in the ordered ferromagnet the spontaneous magnetization $m_S$ occurs:
\begin{equation} \tag{a4} m _ { s } = \operatorname { lim } _ { H \rightarrow 0 } m ( T , H ) > 0. \end{equation}
This is an example of spontaneous symmetry breaking: $\mathcal{H}$ for $H = 0$ does not single out a sign of $m$ (replacing all $\{ S _ { i } \}$ by $\{ - S _ { i } \}$ leaves $\mathcal{H}$ invariant). However, for $T < T _ { c }$ and $H = 0$ the equilibrium state of the system is two-fold degenerate ($\pm m _ { s }$). This degeneracy is already obvious from the groundstate of (a1), for $T \rightarrow 0$, found from the absolute minimum of $H$ as a functional of the $\{ S _ { i } \}$: for $H = 0$ this minimum occurs for either all $S _ { i } = + 1$ or all $S _ { i } = - 1$.
Interestingly, for $d = 1$ no such phase transition at $T _ { c } > 0$ occurs; rather $T _ { c } = 0$ [a1]. The problem (a1)–(a3) is solved exactly by transfer matrix methods [a3]. Rewriting (a1) as $H = - J \sum _ { i = 1 } ^ { N } S _ { i } S _ { i+ 1 } - {\cal H} \sum _ { i = 1 } ^ { N } S _ { i }$ with the periodic boundary condition $S _ { N + 1 } = S _ { 1 }$, one finds
\begin{equation} \tag{a5} Z = \sum _ { S _ { 1 } = \pm 1 } \ldots \sum _ { S _ { N } = \pm 1 } \end{equation}
\begin{equation*} \operatorname { exp } \left\{ \frac { 1 } { k _ { B } T } \sum _ { i = 1 } ^ { N } [ J S _ { i } S _ { i+ 1 } + \frac { H } { 2 } ( S _ { i } + S _ { i+ 1 } ) ] \right\} = \end{equation*}
\begin{equation*} = \sum _ { S _ { 1 } = \pm 1 } \cdots \sum _ { S _ { N } = \pm 1 } \prod _ { i = 1 } ^ { N } \end{equation*}
\begin{equation*} \operatorname { exp } \left\{ \frac { 1 } { k _ { B } T } \left[ J S _ { i } S _ { i + 1 } + \frac { H } { 2 } ( S _ { i } + S _ { i + 1 } ) \right] \right\} = \end{equation*}
\begin{equation*} = \sum _ { S _ { 1 } = \pm 1 } \ldots \sum _ { S _ { N } = \pm 1 } \prod _ { i = 1 } ^ { N } \langle S _ { i } | \mathcal{P} | S _ { i+ 1 } \rangle \end{equation*}
The $( 2 \times 2 )$-matrix ${\cal P} = ( P _ { s s ^ { \prime } } ) = ( \langle S | {\cal P} | S ^ { \prime } \rangle )$ is defined as
\begin{equation} \tag{a6} \mathcal{P} \equiv \left( \begin{array} { c c } { \operatorname { exp } \left( \frac { J + H } { k _ { B } T } \right) } & { \operatorname { exp } \left( \frac { - J } { k _ { B } T } \right) } \\ { \operatorname { exp } \left( \frac { - J } { k _ { B } T } \right) } & { \operatorname { exp } \left( \frac { J - H } { k _ { B } T } \right) } \end{array} \right). \end{equation}
Now $Z$ is simply the trace of an $N$-fold matrix product,
\begin{equation} \tag{a7} Z = \sum _ { S _ { 1 } = \pm 1 } \left( S _ { 1 } | \mathcal{P} ^ { N } | S _ { 1 } \right) = \lambda _ { + } ^ { N } + \lambda ^ { N }_{-}, \end{equation}
where the property was used that the trace of a symmetric matrix is independent of the representation, and so one can evaluate the trace by first diagonalizing $\mathcal{P}$,
\begin{equation} \tag{a8} \mathcal{P} = \left( \begin{array} { c c } { \lambda _ { + } } & { 0 } \\ { 0 } & { \lambda _ { - } } \end{array} \right) , \quad \mathcal{P} ^ { N } = \left( \begin{array} { c c } { \lambda _ { + } ^ { N } } & { 0 } \\ { 0 } & { \lambda ^ { N } } \end{array} \right), \end{equation}
where the eigenvalues $\lambda _ { + }$, $\lambda_{-}$ are found from the vanishing of the determinant, $\operatorname { det } ( \mathcal{P} - \lambda \mathcal{I} ) = 0$, $\cal I$ being the unit $( 2 \times 2 )$-matrix:
\begin{equation} \tag{a9} \lambda _ { \pm } = \operatorname { exp } \left( \frac { J } { k _ { B } T } \right) \operatorname { cosh } \left( \frac { H } { k _ { B } T } \right) \pm \end{equation}
\begin{equation*} \pm \left[ \operatorname { exp } ( \frac { 2 J } { k _ { B } T } ) \operatorname { cosh } ^ { 2 } ( \frac { H } { k _ { B } T } ) - 2 \operatorname { sinh } ( \frac { 2 J } { k _ { B } T } ) \right] ^ { 1 / 2 }. \end{equation*}
In the limit $N \rightarrow \infty$ the largest eigenvalue dominates, $Z \rightarrow \lambda _ { + } ^ { N } $, and hence
\begin{equation} \tag{a10} F = - k _ { B } T \operatorname { ln } \lambda _ { + } = \end{equation}
\begin{equation*} = - J - k _ { B }T \operatorname { ln } \left\{ \operatorname { cosh } \left( \frac { H } { k _ { B } T } \right) + + \left[ \operatorname { sinh } ^ { 2 } \left( \frac { H } { k _ { B } T } \right) + \operatorname { exp } \left( - \frac { 4 J } { k _ { B } T } \right) \right] ^ { 1 / 2 } \right\}, \end{equation*}
\begin{equation} \tag{a11} m = \frac { \operatorname { sinh } \left( \frac { H } { k _ { B } T } \right) } { [ \operatorname { sinh } ^ { 2 } \left( \frac { H } { k _ { B } T } \right) + \operatorname { exp } \left( - \frac { 4 J } { k _ { B } T } \right) ] ^ { 1 / 2 } }. \end{equation}
Indeed, for $T > 0$ there is no spontaneous magnetization, and for $H \rightarrow 0$ the susceptibility becomes $\chi = ( k _ { B } T ) ^ { - 1 } \operatorname { exp } ( 2 J / k _ { B } T )$.
It is remarkable that (a11) strongly contradicts the popular molecular field approximation (MFA). In the molecular field approximation one replaces in the interaction of every spin $S _ { i }$ with its neighbours, $[ S _ { i } ( S _ { i - 1 } + S _ { i + 1 } ) ]$, the spins by their averages, $S _ { i - 1 } \rightarrow \langle m \rangle$; $S_{i + 1 }\rightarrow \langle m \rangle$, the problem becomes a single-site Hamiltonian where $S _ { i }$ is exposed to an effective field $H _ { \text{eff} } = H + 2 m J$, which needs to be calculated self-consistently; carrying out the average over the two states $S _ { i } = \pm 1$ one finds
\begin{equation} \tag{a12} m = \frac { \operatorname { exp } \Bigl( \frac { H _ { \text{eff} } } { k _ { B } T }\Bigr ) - \operatorname { exp } \Bigl( - \frac { H _ {\text{eff} } } { k _ { B } T }\Bigr ) } { \operatorname { exp }\Bigl ( \frac { H _ { \text{eff} } } { k _ { B } T }\Bigr ) + \operatorname { exp } \Bigl( - \frac { H _ { \text{eff} } } { k _ { B } T } \Bigr) } = \end{equation}
\begin{equation*} = \operatorname { tanh } [ \frac { H + 2 m J } { k _ { B } T } ], \end{equation*}
which yields $T _ { c } = 2 J / k _ { B }$ and $m _ { s } \propto ( 1 - T / T _ { c } ) ^ { \beta }$ with a critical exponent $\beta = 1 / 2$, and a Curie–Weiss law for $\chi ( \chi \propto ( T / T _ { c } - 1 ) ^ { - \gamma } \text { with } \gamma = 1 )$. Thus, the Ising model shows that the molecular field approximation in this case yields unreliable and misleading results!
For the Ising-model in $d = 2$, exact transfer matrix methods are applicable for $H = 0$; they show that a phase transition at $T _ { c } > 0$ does exist [a3], [a4], [a5]. But the critical exponents $\beta$, $\gamma$ differ very much from their molecular field approximation values; namely, $\beta = 1 / 8$ and $\gamma = 7 / 4$. This is important, since the exponents $\beta = 1 / 2$ and $\gamma = 1$ also follow from the Landau theory of phase transitions [a2], which only requires that $F$ can be expanded in a power series in $m$, with the coefficient at the $m ^ { 2 }$ term changing sign at $T _ { c }$ as $T / T _ { c } \rightarrow 1$, which are plausible assumptions on many grounds. The $d = 2$ Ising model testifies that neither molecular field approximation nor Landau theory are correct. The Ising model then prompted the development of entirely new theoretical concepts, namely renormalization group analysis [a6], by which one can understand how non-mean-field critical behaviour arises. The Ising model also became a very useful testing ground for many numerical methods: e.g. systematic expansions of $F$ at low $T$ (in the variable $u = \operatorname { exp } ( - 4 J / k _ { B } T )$) or at high $T$ in the variable $v = \operatorname { tanh } ( J / k _ { B } T )$ [a7], or Monte-Carlo methods [a8]. It also played a pivotal role for the concepts on surface effects on phase transitions, and for phase coexistence (domains of oppositely oriented magnetization, separated by walls). Such problems were described with a mathematical rigor that is seldomly found in the statistical thermodynamics of many-body systems. Rigorous work includes the existence of a spontaneous magnetization for $d \geq 2$ ( "Peierls proof" ), inequalities between spin correlations, theorems on the zeros of the partition function, etc.; see [a9]. The Ising model is the yardstick against which each new approach is measured.
Finally, there are extensions of the Ising model. One direction is to make the $J _ {i j }$ more complicated rather than uniformly ferromagnetic ($J _ { i j } > 0$). E.g., if in one lattice direction $J _ { 1 } > 0$ between nearest neighbours but $J _ { 2 } < 0$ between next nearest neighbours, the resulting anisotropic next nearest neighbour Ising model (ANNNI model) is famous [a10] for its phase diagram with infinitely many phases and transitions; choosing the $J _ { i j } = \pm J$ at random from a prescribed distribution, the resulting Ising spin glass [a11] is a prototype model of glasses and other disordered solids.
Another extension adds "time t" as a variable: by a transition probability $w ( \{ S _ { i } \} \rightarrow \{ S _ { i } ^ { \prime } \} )$ per unit time one is led to a master equation for the probability that a state $\{ S _ { 1 } , \ldots , S _ { N } \}$ occurs at time $t$. Such kinetic Ising models [a12] are most valuable to test concepts of non-equilibrium statistical mechanics, and provide the basis for simulations of unmixing in alloys ( "spinodal decomposition" ), etc. Finally, one can generalize the Ising model by replacing the spin $S _ { i } = \pm 1$ by a more complex variable, e.g. in the Potts model [a13] each site may be in one of $p$ states where $p$ is integer (also, the limit $p \rightarrow 1$ is of interest; the so-called "percolation problem" [a14]). The techniques for the Ising model (transfer matrix, series expansions, renormalization, Monte Carlo, etc.) are valuable for all these related problems, too.
References
| [a1] | E. Ising, "Beitrag zur Theorie des Ferromagnetismus" Z. Phys. , 31 (1925) pp. 253–258 |
| [a2] | L.D. Landau, E.M. Lifshitz, "Statistical physics" , Pergamon (1958) |
| [a3] | R.J. Baxter, "Exactly solved models in statistical mechanics" , Acad. Press (1982) |
| [a4] | L. Onsager, "Crystal statistics I. A two-dimensional model with an order-disorder transition" Phys. Rev. , 65 (1944) pp. 117–149 |
| [a5] | B.M. McCoy, T.T. Wu, "The two-dimensional Ising model" , Harvard Univ. Press (1973) |
| [a6] | M.E. Fisher, "The renormalization group in the theory of critical behavior" Rev. Mod. Phys. , 46 (1974) pp. 597–616 |
| [a7] | "Phase Transitions and Critical Phenomena" C. Domb (ed.) M.S. Green (ed.) , 3 , Acad. Press (1974) |
| [a8] | "Monte Carlo methods in statistical physics" K. Binder (ed.) , Springer (1979) |
| [a9] | R.B. Griffiths, "Rigorous results and theorems" C. Domb (ed.) M.S. Green (ed.) , Phase Transitions and Critical Phenomena , 1 , Acad. Press (1972) pp. 7–109 |
| [a10] | W. Selke, "The Annni model-theoretical analysis and experimental application" Phys. Rep. , 170 (1988) pp. 213–264 |
| [a11] | K. Binder, A.P. Young, "Spin glasses: experimental facts, theoretical concepts, and open questions" Rev. Mod. Phys. , 58 (1986) pp. 801–976 |
| [a12] | K. Kawasaki, "Kinetics of Ising models" C. Domb (ed.) M.S. Green (ed.) , Phase Transitions and Critical Phenomena , 2 , Acad. Press (1972) pp. 443–501 |
| [a13] | F.Y. Wu, "The Potts model" Rev. Mod. Phys. , 54 (1982) pp. 235–268 |
| [a14] | D. Stauffer, A. Aharony, "Introduction to percolation theory" , Taylor&Francis (1992) |
Ising model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ising_model&oldid=15668