Irregular prime number
An odd prime number  for which the number of classes of ideals in the cyclotomic field
for which the number of classes of ideals in the cyclotomic field  is divisible by
is divisible by  . All other odd prime numbers are called regular.
. All other odd prime numbers are called regular.
Kummer's test allows one to solve for each given prime number the problem of whether it is regular or not: For an odd prime number to be regular it is necessary and sufficient that none of the numerators of the first  Bernoulli numbers
Bernoulli numbers  is divisible by
is divisible by  (cf. [1]).
(cf. [1]).
The problem of the distribution of regular and irregular prime numbers arose in this connection. Tables of the Bernoulli numbers and Kummer's test indicated that among the first hundred there are only three irregular prime numbers, 37, 59, 67 (the numerators of  ,
,  and
and  are multiples of 37, 59 and 67, respectively). E. Kummer conjectured that there are on the average twice as many regular prime numbers as irregular ones. Later C.L. Siegel [2] conjectured that the ratio of irregular prime numbers to regular prime numbers contained in an interval
are multiples of 37, 59 and 67, respectively). E. Kummer conjectured that there are on the average twice as many regular prime numbers as irregular ones. Later C.L. Siegel [2] conjectured that the ratio of irregular prime numbers to regular prime numbers contained in an interval 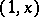 tends to
tends to 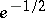 as
as 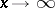 (here
(here  is the base of natural logarithms). Up till now (1989) it is only known that the number of irregular prime numbers is infinite. There are 439 regular and 285 irregular prime numbers among the odd numbers smaller than 5500, cf. [3].
is the base of natural logarithms). Up till now (1989) it is only known that the number of irregular prime numbers is infinite. There are 439 regular and 285 irregular prime numbers among the odd numbers smaller than 5500, cf. [3].
For any regular  the Fermat equation
the Fermat equation
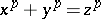 |
does not have non-zero solutions in the rational numbers [1].
Let 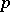 be an irregular prime number, let
be an irregular prime number, let 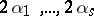 be the indices of the Bernoulli numbers among
be the indices of the Bernoulli numbers among 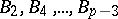 whose numerators are divisible by
whose numerators are divisible by 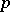 and let
and let  and
and 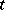 be natural numbers such that
be natural numbers such that 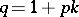 is a prime number smaller than
is a prime number smaller than 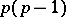 and
and 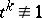
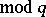 . Let
. Let
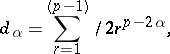 |
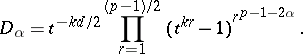 |
If for each 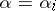 ,
,  ,
,
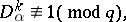 |
then for the irregular prime number 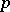 Fermat's theorem holds, i.e. the Fermat equation is unsolvable in the non-zero rational numbers. This is called Vandiver's test. The truth of Fermat's theorem for all exponents smaller than 5500 has been proved by using Vandiver's test (cf. [4]).
Fermat's theorem holds, i.e. the Fermat equation is unsolvable in the non-zero rational numbers. This is called Vandiver's test. The truth of Fermat's theorem for all exponents smaller than 5500 has been proved by using Vandiver's test (cf. [4]).
References
| [1] | E. Kummer, "Allgemeiner Beweis des Fermat'schen Satzes, dass die Gleichung 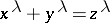 durch ganze Zahlen unlösbar ist, für alle diejenigen Potentz-Exponenten durch ganze Zahlen unlösbar ist, für alle diejenigen Potentz-Exponenten 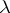 , welche ungerade Primzahlen sind und in den Zählern der ersten , welche ungerade Primzahlen sind und in den Zählern der ersten 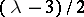 Bernoulli'schen Zahlen als Factoren nicht Vorkommen" J. Reine Angew. Math. , 40 (1850) pp. 130–138 Bernoulli'schen Zahlen als Factoren nicht Vorkommen" J. Reine Angew. Math. , 40 (1850) pp. 130–138 |
| [2] | C.L. Siegel, "Zu zwei Bemerkungen Kummers" Nachr. Akad. Wiss. Göttingen Math. Phys. Kl. , 6 (1964) pp. 51–57 |
| [3] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [4] | H.S. Vandiver, "Examination of methods of attack on the second case of Fermat's last theorem" Proc. Nat. Acad. Sci. USA , 40 : 8 (1954) pp. 732–735 |
Comments
The truth of Fermat's theorem has been established for all exponents  by S. Wagstaff [a1].
by S. Wagstaff [a1].
His computations show that 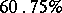 of the 11733 odd prime numbers smaller than
of the 11733 odd prime numbers smaller than 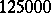 are regular. This is in close agreement with Siegel's conjecture, which expects
are regular. This is in close agreement with Siegel's conjecture, which expects 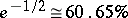 of all prime numbers to be regular.
of all prime numbers to be regular.
More generally, one defines the index of irregularity 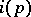 of an odd prime number
of an odd prime number  as the number of indices
as the number of indices 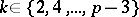 for which
for which 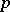 divides the numerator of the Bernoulli number
divides the numerator of the Bernoulli number 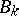 . The regular prime numbers are the prime numbers
. The regular prime numbers are the prime numbers 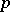 satisfying
satisfying 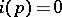 . Heuristically, one expects the fraction of prime numbers
. Heuristically, one expects the fraction of prime numbers 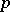 for which
for which  to be
to be 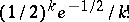 , and this is confirmed by the data in [a1]. It was proved by Eichler that the first case of Fermat's theorem holds for a prime exponent
, and this is confirmed by the data in [a1]. It was proved by Eichler that the first case of Fermat's theorem holds for a prime exponent  when
when 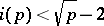 (cf. [a2]). See also Fermat great theorem.
(cf. [a2]). See also Fermat great theorem.
References
| [a1] | S. Wagstaff, "The irregular primes to 125,000" Math. Comp. , 32 (1978) pp. 583–591 |
| [a2] | L.C. Washington, "Introduction to cyclotomic fields" , Springer (1982) |
| [a3] | H.M. Edwards, "Fermat's last theorem. A genetic introduction to algebraic number theory" , Springer (1977) |
| [a4] | S. Lang, "Cyclotomic fields" , 1–2 , Springer (1978–1980) |
Irregular prime number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Irregular_prime_number&oldid=18479