Inversion of an elliptic integral
The problem of constructing the function  as a function of
as a function of  or of constructing single-valued composite functions of the form
or of constructing single-valued composite functions of the form  in the case of an elliptic integral
in the case of an elliptic integral
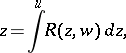 |
where  is a rational function of variables
is a rational function of variables  and
and  which are related by the equation
which are related by the equation  , where
, where  is a polynomial of degree 3 or 4 without multiple roots. The complete solution of this problem was given almost simultaneously in 1827–1829 by N.H. Abel and C.G.J. Jacobi, who showed that its solution led to new transcendental elliptic functions (cf. Elliptic function).
is a polynomial of degree 3 or 4 without multiple roots. The complete solution of this problem was given almost simultaneously in 1827–1829 by N.H. Abel and C.G.J. Jacobi, who showed that its solution led to new transcendental elliptic functions (cf. Elliptic function).
An essentially different approach to the theory of elliptic functions is due to K. Weierstrass. For the elliptic integral of the first kind in Weierstrass normal form,
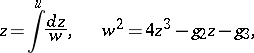 |
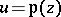 turns out to be the Weierstrass
turns out to be the Weierstrass 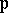 -function with invariants
-function with invariants  (see Weierstrass elliptic functions). For the elliptic integral of the first kind in Legendre normal form,
(see Weierstrass elliptic functions). For the elliptic integral of the first kind in Legendre normal form,
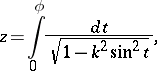 |
inversion leads to the Jacobi elliptic functions.
References
| [1] | N.I. Akhiezer, "Elements of the theory of elliptic functions" , Amer. Math. Soc. (1990) (Translated from Russian) |
| [2] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) pp. Chapt. 3, Abschnitt 2 |
Inversion of an elliptic integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inversion_of_an_elliptic_integral&oldid=19005